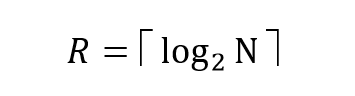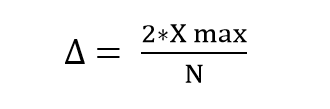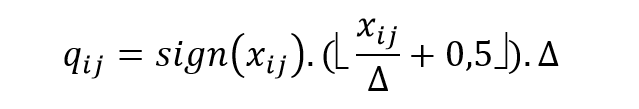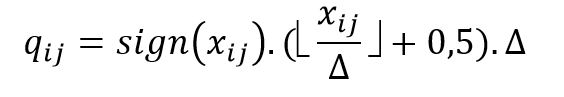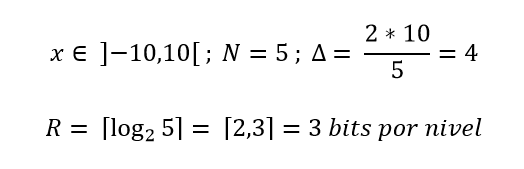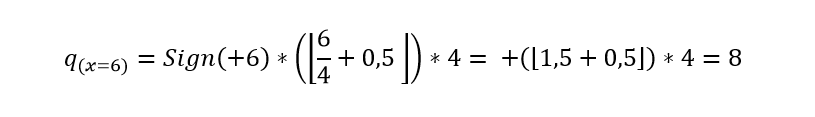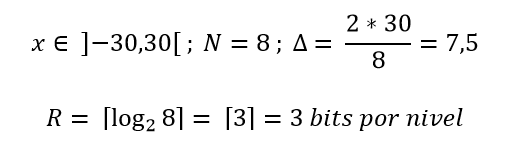Enquadramento

Para armazenar ou transferir conteúdo multimédia, devido ao elevado tamanho destes conteúdos, temos de recorrer a métodos de compressão. Entre estes métodos existem métodos de compressão sem perdas e com perdas. No que aos métodos de compressão com perdas diz respeito, podemos salientar que as respetivas perdas ocorrem somente no quantificador. Estas, na maioria das vezes não são detetáveis pelos sentidos humanos, o que significa que se retirarmos a informação correta podemos obter o mesmo conteúdo multimédia, mas com uma taxa compressão claramente superior.

Introdução

Neste documento será abordada a quantificação escalar uniforme. Este é um dos métodos utilizados na compressão multimédia com introdução de perdas de informação. Como tal, este método aplica a retirada de informação não relevante com o objetivo de comprimir o ficheiro em questão. Esta informação retirada, como referido anteriormente, não é percetível aos sentidos humanos e traduz um diminuo de tamanho considerável o que se traduz numa vantagem quer para armazenamento, quer para transferência via ligação de rede.

Objetivos do trabalho

O objetivo deste trabalho é a compreensão e demonstração de um dos métodos que está presente em muitos codecs que utilizamos nos dias de hoje, e deste modo perceber como ele funcionam e porque funcionam deste modo.

Este trabalho baseia-se em perceber o porquê dos codecs utilizarem estas metodologias e qual o seu poder de modificação do ficheiro multimédia original (com elevada qualidade) para um ficheiro de semelhante qualidade, mas comprimido.

Justificação

Compressão recorrendo a quantificador (compressão com perdas) é sem divida o mecanismo mais utilizado hoje em dia, devido ao seu grande nível de compressão.

Um dos exemplos de formatos que utilizam este mecanismo e é bem conhecido por todos nos é o caso do MP3, que é o formato mais utilizado a nível de áudio, apesar de não ser o que mantem o som com a melhor qualidade.

Áreas de aplicação

Podemos encontrar este tipo de quantificador no JPEG que é um formato de imagem que é bem conhecido por todos nós.

Na aplicação do DCT ao JPEG, este pode utilizar um quantificador escalar uniforme para quantificação dos seus valores, pois tem elevada compressão na quantificação de zeros, que segundo referências bibliográficas é muito utilizado.

Quantificação escalar uniforme

Este tipo de quantificação inicia-se pela repartição dos valores de entrada por intervalos de quantificação com largura fixa com a possível exceção dos intervalos dos extremos.

Fronteiras de decisão do quantificador -> Limites dos intervalos de quantificação

Valor médio -> Valores de entrada que se situam dentro de cada intervalo são substituídos pelo valor médio desse mesmo intervalo.

Passo de quantificação (Δ) -> Largura de cada intervalo

Este método contém dois tipos que são o quantificador midrise (Figura 1) e o quantificador midtread (Figura 2), tendo de definir o número de níveis de quantificação para decidir o tipo de quantificação que deve ser aplicar. Se escolhermos número par de níveis iremos adotar o quantificador midrise (Figura 1), no caso contrário estaremos a escolher o quantificador midtread (Figura 2).

Estes dois tipos distinguem-se também pela utilização do valor zero. Em relação ao midtread (Figura 2) podemos ter como valor quantificado à saída este mesmo valor em que a sua utilização é vantajosa quando temos vários valores perto de zero.

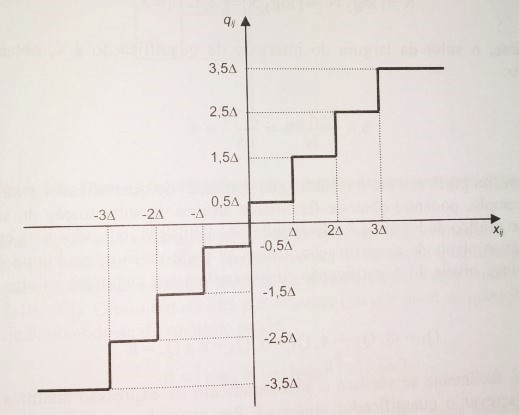
Midrise

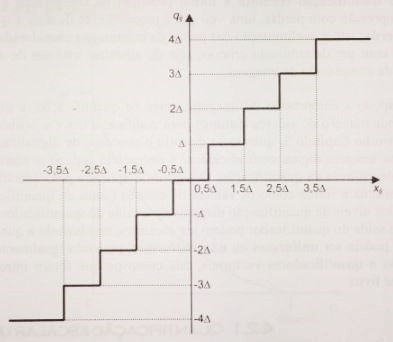
Midtread

Na obtenção de um quantificador escalar uniforme com N níveis de quantificação, cada nível de quantificação necessita de ser representado por R bits que pode ser calculado através da seguinte expressão.

Nota: os parenteses apresentados na formula representam o número inteiro mais próximo arredondado por excesso.

A obtenção da largura de cada intervalo de quantificação é obtida da seguinte forma, onde os valores de entrada se distribuem no intervalo :

Deste modo podemos concluir que as expressões analíticas do processo de quantificação para cada um dos modos são as seguintes:

Midtread:

Midrise:

Nota: os parenteses retos apresentados na formula representam o número inteiro mais próximo arredondado por defeito. A função sign(x_ij) corresponde ao sinal positivo ou negativo do valor de entrada.

Tendo como base estes dois tipos de quantificadores escalares uniformes, temos de salientar que o objetivo principal é minimizar a distorção, ou erro que se introduz quando se quantifica um conjunto de valores de entrada, substituindo-os por um conjunto menor de N valores de saída quantificados.

A minimização destes erros faz-se através da expressão apresentada anteriormente, ajustando o valor do passo de quantificação de modo a corresponder á distribuição dos valores de entrada.

Quando consideramos um conjunto de valores de entrada este erro de quantificação introduzido pelo quantificador, designa-se por distorção granular, e para saber este erro temos de ter em conta que os valores de saída correspondem ao ponto médio de cada um dos intervalos em que se divide os valores de entrada.

A obtenção da distorção granulada pode ser obtida através da seguinte expressão:

Nota: nesta expressão i varia desde i = 1 até i = N/2 para a parte positiva e outros tantos para a negativa.

O erro de quantificação situar-se-á sempre dento do intervalo [-Δ/2, +Δ/2] o que significa que nunca será maior que Δ/2 nem menor do que – Δ/2.

Deste modo podemos calcular facilmente o valor do ruído através da seguinte expressão: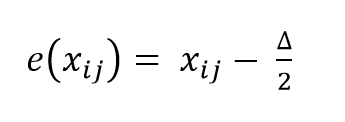Exemplo de aplicação

Como exemplo de aplicação vamos considerar o problema utilizado em sala de aula para a explicação desta técnica de quantificação.

Problema 1:

Pretende-se quantificar um conjunto de resíduos com um quantificador midthread de 5 níveis, sabendo que os resíduos variam no intervalo . Mostre o diagrama:

Resolução:

Problema 2:

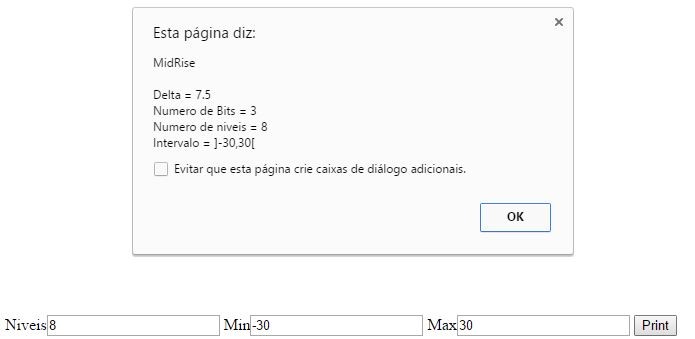
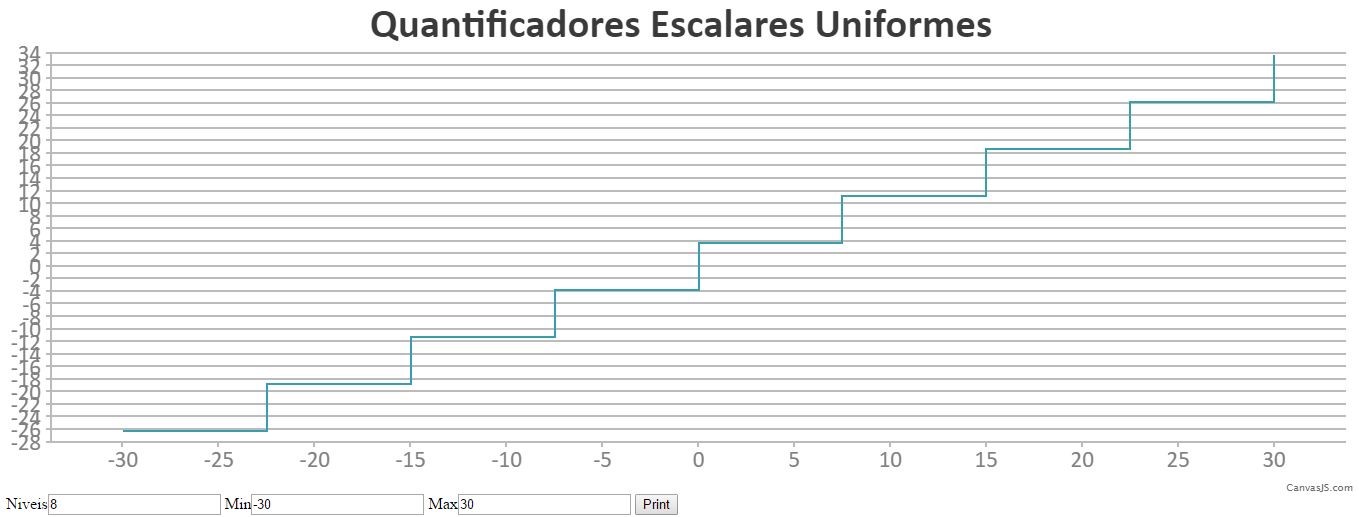
Vendo agora um exemplo para o midrise, utilizando um N = 8 e um intervalo

Resolução:

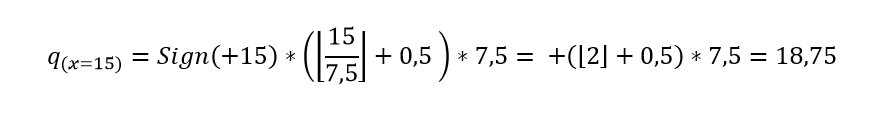Implementação do algoritmo “Quantificação escalar uniforme”

Para a implementação deste algoritmo, como estávamos mais familiarizados com a linguagem de programação JAVA escolhemos esta mesma para base da nossa implementação. Depois de termos todos os cálculos necessários a serem realizados no algoritmo deparamo-nos com a grande dificuldade de desenhar o gráfico em JAVA. Tentamos recorrer a biblioteca do JAVA SWING, onde através desta conseguimos desenhar os eixos do gráfico e os respetivos intervalos, recorrendo a dados inseridos manualmente.

Devido as grandes dificuldades em colocar o algoritmo a mostrar o gráfico somente com a inserção dos dados iniciais mudamos de linguagem de programação para JAVASCIPT.

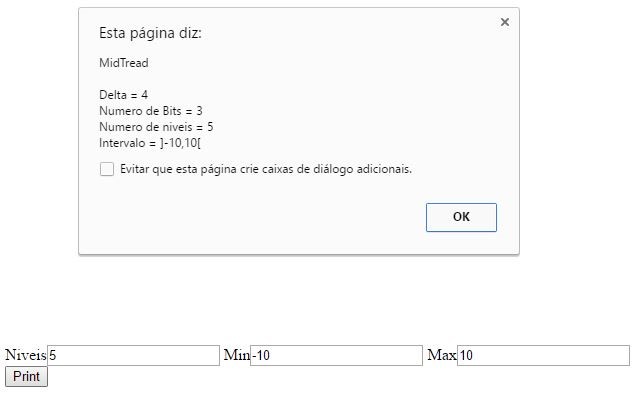
Como já possuímos os códigos de realizar as contas em JAVA, somente tivemos de os adaptar a JAVASCRIPT, algo que fizemos facilmente. O grande problema novamente foi o desenhar do gráfico. Para isso recorremos a biblioteca CANVAS JS onde conseguimos mais facilmente desenhar os gráficos pretendidos, sendo somente necessário inserir o número de níveis e o intervalo no formulário presente no JAVASCRIPT.

Quantificação escalar uniforme em javascript

Comparação com outros métodos semelhantes

O quantificador escalar uniforme é menos trabalhoso de implementar em relação ao quantificador não uniformes, mas tem também um menor desempenho ao nível da codificação que este segundo.

Em relação as vantagens desta implementação, alem de ser mais simples de implementar é também mais “leve” a nível de processamento.

Conclusão

Neste artigo ficou demonstrado o funcionamento do quantificador escalar uniforme em ambos os seus métodos de aplicação midtread e midrise.

Este não é o tipo de quantificação que obtém maior compressão, mas é o de mais fácil implementação.

O código desenvolvido foi implementado com o intuito de ajudar no leccionamento desta parte da matéria da disciplina de Multimédia II.

O trabalho foi desenvolvido com êxito e o código JAVASCRIPT segue em anexo a este documento.

Segue também em anexo a tentativa de implementação inicial em JAVA.

Bibliografia

Sayood, K., “Introduction.to.Data.Compression”, Morgan.Kauffman, 2006.

Salomon, D., “A.Concise.Introduction.to.Data.Compression”, Springer, 2008.

Ribeiro, N.,Torres,J.,”Tecnologias Compressão Multimédia”,FCA,2009

Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.

Texto da autoria de Daniel Dias Lima Mendes, Diogo Emanuel Lamas Silva e Nelson José Santos Almeida e revisto por Nuno Magalhães Ribeiro.

Código javascript da autoria de Daniel Dias Lima Mendes, Diogo Emanuel Lamas Silva e Nelson José Santos Almeida

Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas Silva e Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.