Introdução

Trata-se de um algoritmo que utiliza modos de compressão sem perdas, uma vez que não considera a semântica da informação a codificar, o que permite categoriza-lo como um algoritmo codificador de entropia.

A abordagem utilizada por este algoritmo é a Técnica de Codificação Estatística, uma das técnicas mais eficiente para a codificação de entropia, conferindo igual complexidade à compressão e descompressão da informação, sendo que a implementação algorítmica é a codificação de comprimento variável.

Áreas de aplicação

O método de Compressão Shannon-Fano foi o primeiro a ser desenvolvido, utilizando um compressão sem perdas e uma codificação de tamanho variável para cada um dos símbolos de informação, em que o comprimento do código utilizado é obtido através da frequência de ocorrência desse símbolo da totalidade de informação a ser codificada. Trata-se de um método bastante eficiente e prático, no entanto gera resultados sub-otimos, razão pela qual a sua aplicação prática é quase nula em relação ao método de Compressão Huffman que obtém um resultado ótimo fruto do algoritmo desenvolvido que constrói a árvore binária bottom-up, o que transforma a sua aplicabilidade na codificação de entropia aplicando-se nas normas JPEG e MPEG bem como na norma de FAX. O fato de não considerar o tipo de dados permite que seja utilizado no processo de compressão de outros métodos, para atingir resultados de compressão melhores.

O algoritmo de Shannon-Fano

Shannon-Fano trata-se de um algoritmo de codificação de entropia, uma vez que efetua uma compressão sem perdas, o que corresponde ao melhoramento da eficiência de representação da informação digital, sendo indiferente do tipo de dados a comprimir, representando uma codificação da informação com códigos de tamanho variável.

Codificação

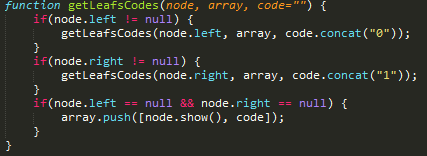
O Algoritmo de Shannon-Fano começa por ordenar os símbolos que representam a informação de acordo com a respetiva frequência de ocorrência, para que posteriormente vá dividindo os símbolos de uma forma recursiva, em 2 subconjuntos, cada um contendo os símbolos, cuja soma da frequência de ocorrência seja aproximadamente igual. Esta operação será repetida até que cada subconjunto contenha apenas um e um só símbolo. Esta operação permitirá a construção de uma árvore binária através de uma abordagem “Top-down”, a obtenção do código binário de Shannon-Fano, que será usado para a compressão dos dados originais.

Em baixo encontra-se em pseudo código do algoritmo de codificação:

Descodificação

A descodificação utilizada aqui foi a de bits em série, que consiste nos passos seguintes:

1 – Ler o fluxo de bits comprimidos, bit após bit, e percorrer a tabela final até que se atinja o símbolo correspondente.

2 – À medida que cada conjunto de bits do fluxo comprimido é utilizado, deverá ser descartado. Quando encontra o símbolo correspondente, o descodificador de Shannon-Fano coloca na saída esse mesmo símbolo.

3 – Repetir os passos 1 e 2 até que os bits do fluxo comprimido tenham sido todos processados e descartados.

Em baixo encontra-se em pseudo código do algoritmo de descodificação:

Exemplo de aplicação

O exemplo que vai ser desenvolvido nesta secção, de modo, a demonstrar o funcionamento das partes de codificação e descodificação do algoritmo de Shannon-Fano, terá como principal objetivo permitir demonstrar detalhadamente todos os passos que o algoritmo executa para codificar e posteriormente descodificar o texto introduzido.

Desta forma, será inicialmente introduzido pelo utilizador, um texto para ser codificado, em seguida será apresentada a tabela inicial, utilizada para a obtenção da árvore binária e da tabela final. Após obtida a tabela final será atribuído um código binário a cada caracter do texto inserido, obtendo assim a mensagem codificada.

A descodificação será realizada com recurso ao fluxo de bits comprimidos e à tabela final que contém os códigos binários correspondentes a cada símbolo. Só assim será possível descodificar o fluxo de bits comprimidos e obter o texto originalmente introduzido.

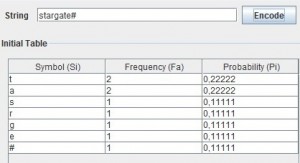
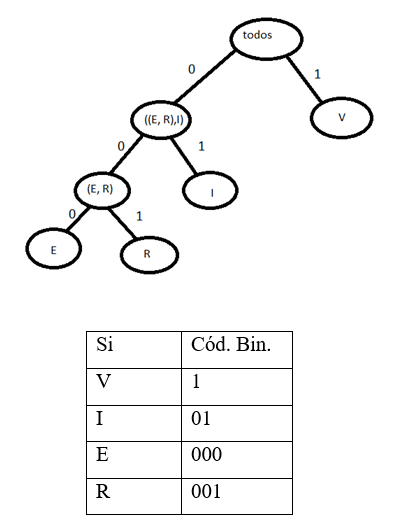
Pretende-se então codificar a sequência “stargate#”, de forma a testar o funcionamento do algoritmo de Shannon-Fano.

Codificação

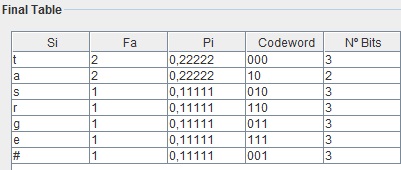
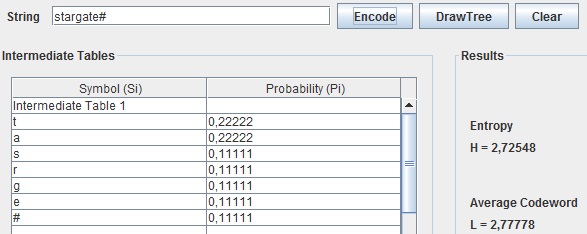
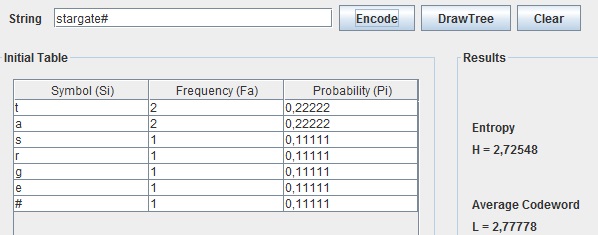
Através da utilização do exemplo acima apresentado, o algoritmo de Shannon-Fano vai, para a codificação, calcular a frequência de ocorrência de cada caracter e de acordo com essa frequência vai ordenar numa tabela os caracteres, colocando na primeira posição o caracter com maior probabilidade e na última posição, o de menor probabilidade (ver Tabela abaixo).

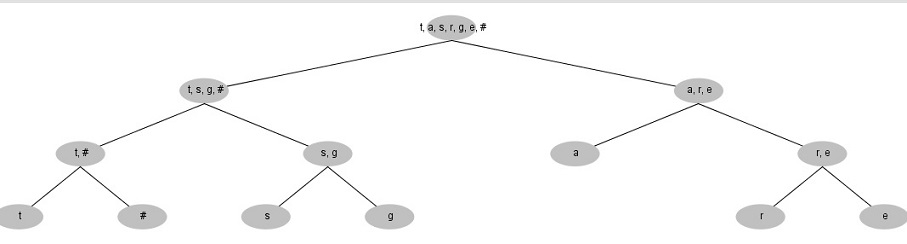
Após a tabela estar ordenada, o algoritmo começa a subdividir, de uma forma recursiva, os símbolos em dois conjuntos de modo a que cada um destes subconjuntos contenha símbolos em que a soma das suas frequências de ocorrências seja o mais aproximado possível. Esta divisão é feita colocando inicialmente, os dois símbolos com maior frequência de ocorrência um em cada subconjunto e de forma recursiva irá comparar a frequência total de cada subconjunto e colocar o próximo símbolo no que tiver a menor frequência.

Neste momento da codificação temos a raiz da árvore binária, o texto de exemplo, a subárvore esquerda e a subárvore direita, os dois subconjuntos, no qual o conjunto que possuir uma maior frequência será o da subárvore esquerda. A partir daqui o algoritmo irá processar cada subárvore de forma recursiva até que cada subconjunto possua apenas um único símbolo, assim como atribuir o bit 0 aos ramos da esquerda da árvore e o bit 1 aos ramos da direita.

Quando for obtida a árvore binária completa será atribuído um código binário a cada símbolo, código esse que será obtido através da junção dos bits correspondentes aos ramos que serão percorridos na travessia da árvore desde a sua raiz até ao símbolo correspondente (ver Tabela abaixo).

Descodificação

Para procedermos à descodificação utilizámos o resultado obtido na codificação anterior. Em seguida é percorrido, o fluxo de bits comprimidos, bit após bit. Para ser possível obter o texto original após a descodificação foi feita uma concatenação de bit após bit e simultaneamente são consultados os códigos de cada símbolo presentes na tabela final, aqui sempre que existe uma correspondência é guardado o símbolo e é descartado o fluxo de bits lido. Este processo é repetido até que todo o fluxo de bits comprimidos tenha sido processado e descartado.

Desta forma, a partir do fluxo de bits comprimidos é obtido o texto original correspondente, como é possível verificar na imagem abaixo apresentada.

Implementação do algoritmo Shannon-Fano em java

É apresentado no quadro abaixo uma parte do código que foi implementado de forma a desenvolver a codificação de Shannon-Fano. O método “buildTree” com base no conteúdo da raiz da árvore, vai percorre-la caracter a caracter e realizar o balanceamento da árvore. Este balanceamento vai ser feito de modo a equilibrar a frequência de ocorrência em cada nó da árvore. Se a frequência de ocorrência da subárvore esquerda for menor ou igual à da subárvore direita, então soma a frequência do próximo caracter à esquerda, senão a frequência é somada à direita.
Ao mesmo tempo que é feito o balanceamento da árvore é atribuído o bit zero (0) ao código binário de cada um dos caracteres da subárvore esquerda e o bit 1 para cada um dos caracteres da subárvore direita.

Shannon Fanno e Huffman em java

Implementação do algoritmo de Shannon-Fano em javascript

O algoritmo passa por várias fases até obtermos o resultado final:

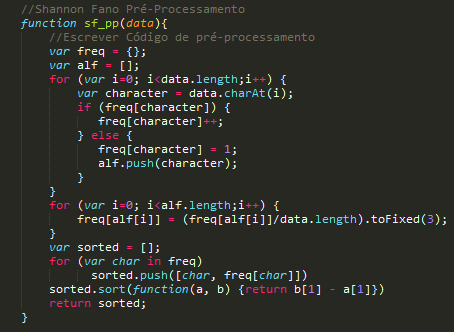
1. É feito um pré-processamento do segmento de texto que o utilizador introduziu, ou seja, conta-se o número de vezes que um caracter aparece na frase dividindo pelo tamanho da mesma obtendo a frequência com que esse mesmo caracter aparece no segmento introduzido.

2. De seguida, constrói-se a árvore onde serão inseridos os elementos na árvore tendo em conta as frequências calculadas anteriormente. Como a divisão não é feita de modo a que os subsegmentos fiquem iguais, mas sim consoante a frequência de cada subsegmento, criamos um algoritmo que indica a posição onde um segmento é partido em 2, para a árvore ficar balanceada em relação às frequências.
Recapitulando, calcula-se a posição onde o segmento é repartido em 2 metades e insere-se cada sub-segmento num novo nó à esquerda ou direita. Neste caso à direita fica sempre o sub-segmento com maior frequência e à esquerda com menor frequência.

3. Após criar a árvore, imprimimos graficamente todos os nós e respetivas arestas utilizando uma biblioteca (Sigma.js) que desenha o conteúdo indicando via JSON as coordenadas e informação a apresentar.
4. Finalmente obtemos o segmento codificado visitando os nós da árvore. Ao visitar cada nó é concatenado o valor consoante a direção. Se for para a esquerda o código é 0, se for para a direita é 1, assim recursivamente.

No final obtém-se a tabela de frequências, a árvore desenhada, a tabela com os códigos binários de cada carater e o segmento comprimido.

Como referido anteriormente, foi utilizado um script externo para desenhar a árvore consoante a informação fornecida ao script. A estrutura da árvore foi uma adaptação da estrutura original de uma árvore BST (Binary Search Tree), para JSON, conforme era pedido pela biblioteca externa (Sigma.js).

Shannon Fanno e Huffman em javascript

Comparação com outros métodos semelhantes

Em comparação com a codificação de Huffman, podemos chegar à conclusão que a melhor codificação de Shannon-Fano é igual à codificação de Huffman. Assim podemos afirmar que a codificação através do algoritmo de Huffman é bastante mais eficaz em relação à de Shannon-Fano, daí que o algoritmo de codificação de Huffman seja o mais utilizado actualmente.

Através das imagens seguintes podemos verificar que em relação ao Shannon-Fano estamos perante a melhor codificação pois o comprimento médio é exactamente igual ao obtido pelo Huffman.

Após obtido o valor do comprimento médio em cada um dos métodos de compressão vamos então calcular o rácio de compressão e o débito binário, para cada um e verificar que vai ser igual, pois ambos possuem o mesmo comprimento médio.

Devido às diferentes árvores que Shannon-Fano pode produzir, nem sempre o resultado é o melhor, mas no seu melhor resultado é equivalente a Huffman.
A abordagem bottom-up de Huffman permite-lhe obter sempre o melhor rácio de compressão.

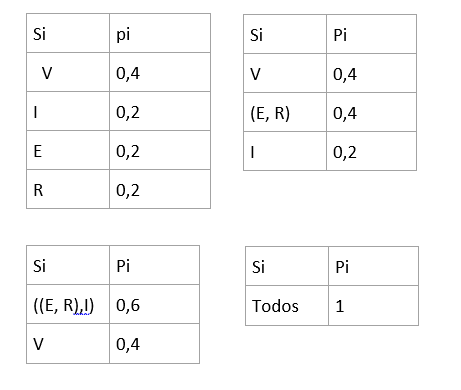
Utilizando outro exemplo com a palavra VIVER:
Melhor código de comprimento fixo para a palavra VIVER é 2bps.

a) Utilizando Shannon-Fano:
Temos que neste caso os códigos são 2bps, ou seja, igual ao melhor código de comprimento fixo. Não obtemos compressão
b) Utilizando Huffman

LHuffman= 1*0,4+2*0,2+3*0,2+3*0,2= 2 bps
Neste caso, como o alfabeto era pequeno e a probabilidade entre os símbolos era muito parecida, a codificação de Huffman não tirou melhor partido, mas mesmo assim quase que toca a Entropia e nos casos em que o alfabeto e as probabilidades sejam mais uniformemente distribuídas, Huffman consegue melhores resultados que o melhor código de comprimento fixo e que Shannon-Fano.

H(s) = 1,92 bps

Bibliografia

• Ribeiro,Nuno e Torres, José, Tecnologias de Compressão Multimédia, 1ª edição, FCA – Editora de Informática, Porto, 2009.
• Salomon, David, Data Compression, 4ª Edição, Springer, Northridge-USA, 2002
• The Prague Stringology Club – http://www.stringology.org/DataCompression/sf/index_en.html
• Wikipédia – http://en.wikipedia.org/wiki/Huffman_coding e http://en.wikipedia.org/wiki/Shannon-Fano_coding.

Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.

Texto da autoria de Joel Correia (nº 28124), Henrique Vieira (nº 28139), Miguel Lopes (nº20575) e revisto por Nuno Magalhães Ribeiro.

Código javascript da autoria de Joel Correia (nº 28124), Henrique Vieira (nº 28139), Miguel Lopes (nº20575).

Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.