Introdução

Neste artigo será abordado o método de codificação multimédia de Huffman – analisando separadamente os respectivos algoritmos de compressão e descompressão – na sua versão estática.

Este método de compressão é um dos mais utilizados na actualidade para compressão de diversos media – maioritariamente como componente de codecs mais complexos (Salomon, 2007) – apesar de ter sido inicialmente desenvolvido para compressão de texto (Pu, 2006).

A sua designação deriva de David Huffman, que desenvolveu o método como projecto da disciplina Teoria da Informação em 1950 (Blelloch, 2001) enquanto aluno de Doutoramento no MIT (Sayood, 2006) (Wikimedia Foundation, Inc., 2016) e publicou as suas conclusões em 1952 no artigo “A Method for the Construction of Minimum-Redundancy Codes” na revista Proceedings of the I.R.E. (Huffman, 1952).

A codificação de Huffman assenta na Teoria de Informação de Shannon (Shannon, 1948) e no subsequente princípio de que, num elemento de informação (texto, imagem, áudio, etc.) representado por símbolos, alguns desses símbolos ocorrem mais vezes que outros. Por conseguinte, se representarmos esses símbolos mais comuns utilizando códigos mais pequenos (usando menos bits) e os símbolos menos frequentes usando códigos mais extensos (com menos bits), contrapondo à representação dos símbolos com códigos de comprimento fixo (como, por exemplo, ASCII), iremos obter uma codificação binária com menos bits, como resultado de uma diminuição do comprimento médio (em bits) de cada código (Huffman, 1952) (Pu, 2006). O algoritmo de Huffman é, portanto, baseado na categoria de Codificação de Entropia – a informação é encarada como uma sequência de símbolos genéricos, menosprezando a semântica dos mesmos -, sendo um modo de codificação sem perdas – o código resultante é totalmente reversível, ou seja, a sua descodificação resulta num fluxo de dados exactamente igual ao fluxo de dados de origem (Ribeiro, Apontamentos das Aulas, 2016).

 Áreas de aplicação

Este método de codificação tem, como supracitado, uma ampla utilização nas tecnologias multimédia. Sendo um algoritmo que permite optimizar a informação sem qualquer tipo de perdas, é extremamente empregue como “passo” final do processamento de dados em normas como JPEG (norma muito utilizada na compressão de imagem) ou MPEG (aplicada a vídeo) ou ainda em GZIP (compressão de ficheiros) (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007) (Blelloch, 2001).

Regra geral, a codificação de Huffman é aplicada como bloco final de uma sequência de diversos blocos aplicados na norma. Por exemplo, na codificação de uma imagem usando a norma JPEG, poderemos esquematizar os componentes de processamento da seguinte forma:

Img 1 – Diagrama simplificado de componentes de norma JPEG (usando DCT e Huffman), como exemplo de uma aplicação da codificação de Huffman – baseado em (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007)

É igualmente de referir a utilização do codec de Huffman nas normas de fax – recorde-se que, conforme referido na introdução (vide 1. Introdução), Huffman foi inicialmente desenvolvido para codificação de texto, o que o torna um algoritmo de eleição para codificação de documentos de texto como fax.

Huffman é, igualmente, aplicado em codificações de áudio, como CD ou parte da recente norma MP3.

Esta ampla aplicação resulta de 2 factores principais:

a) Huffman é de utilização livre (não patenteado), sendo uma mais-valia por comparação com outros métodos de codificação sem perdas, como a codificação aritmética (Ribeiro, Apontamentos das Aulas, 2016);

b) É extremamente simples, mas simultaneamente muito eficaz na codificação de entropia, permitindo reduzir significativamente a quantidade de bits necessários para codificar qualquer bloco de informação.

O algoritmo de Huffman

Este algoritmo é incluído nos métodos de codificação sem perdas, mais propriamente nos codificadores de entropia, uma vez que se baseia na Teoria de Informação.

Segundo esta Teoria, desenvolvida por Shannon, se considerarmos uma fonte de informação S constituída por símbolos s_i aleatórios – imaginemos um texto (S) constituído por caracteres (s_i) ou uma imagem (S) composta por pixéis com informação de cor (s_i) – e se também considerarmos p_i como a probabilidade de ocorrência desses símbolos (s_i) na fonte (S), então a informação que se obtém na recepção do símbolo (auto-informação) é definida como  (Shannon, 1948) (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007).  é, portanto, o valor de quantidade média de informação contida em s_i. Prosseguindo, e ainda de acordo com Shannon, então a informação média (entropia) da fonte S é definida matematicamente por:

De referir que, sendo aqui perspectivada a aplicação de codificação multimédia, de base binária, então a base logarítmica aplicada nas expressões é igualmente de base 2 – os códigos obtidos assentam em apenas dois símbolos: 0 e 1.

Por conclusão, entropia pode ser definida como o número médio mínimo de bits necessário à representação de cada símbolo (s_i) de uma dada fonte (S), em função da probabilidade de ocorrência desse símbolo na fonte (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007).

Esta definição é crucial, quer como princípio teórico para qualquer algoritmo de codificação, quer como fim a atingir, pois o valor H(S) representa, como anteriormente referido, o número médio mínimo de bits necessário para codificar um símbolo e, portanto, é o valor ideal a atingir no processo de codificação de uma fonte (Ribeiro, Apontamentos das Aulas, 2016).

Assim, desta análise teórica introdutória, percebemos que Huffman baseia a sua codificação na probabilidade (p_i) de ocorrência de cada símbolo (s_i) construindo um código de comprimento variável por símbolo baseado nessas probabilidades. Como Huffman respeita, por inerência, a entropia da fonte, os símbolos com maior probabilidade serão codificados com menos bits e os símbolos menos recorrentes serão codificados com mais bits, pelo que o código final resultante é, em média, muito menor (no que concerne à quantidade de bits empregue na sua representação) do que a fonte (Pu, 2006).

Para que este fundamento possa ser aplicado no algoritmo de Huffman, é necessário existir um modelo de probabilidades de ocorrência de símbolos, o qual poderá ser pré-determinado (derivado de pressupostos) ou então obtido a partir dos dados, calculado através da frequência de ocorrência de cada símbolo, usando-se, para o efeito, um ‘modelador de probabilidades’ (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007) – denote-se que a necessidade de utilização de um modelo de probabilidades provoca, logicamente, um atraso no processamento geral de codificação. É este modelo de probabilidades que servirá de base para o mapeamento de símbolos usado no processo de codificação (Huffman, 1952).

Como se pode inferir do exposto, no algoritmo de Huffman os símbolos são processados e codificados individualmente. Deste modo, para que esta execução seja realizada eficazmente, é aconselhável a aplicação de um pré-processamento aos dados para que haja uma partição correcta dos símbolos da mensagem (Bashkaran & Konstantinides, 1997).

Simplisticamente, a implementação prática da codificação de Huffman assenta na construção de uma árvore binária (mais uma vez, vamos basear a análise aplicada a dados informáticos, mas ressalve-se a possibilidade do algoritmo de Huffman poder ser aplicada a D dígitos (Huffman, 1952)) de símbolos – à semelhança do algoritmo de Shannon-Fano, com a diferença de que em Huffman esta é construída de baixo para cima (bottom-up) – e cuja posição na árvore depende da sua probabilidade. Os ramos esquerdos de cada sub-árvore são codificados com 0 e os da direita com 1 (Pu, 2006) (Li & Drew, 2004). Percorrendo a árvore da raiz até à folha (que contém o símbolo) e concatenando sequencialmente os 0 e 1 de cada ramo percorrido, obtemos o código correspondente a esse símbolo. Esta mesma árvore (ou a tabela equivalente) servirá de base ao processo de descodificação, cujo princípio de funcionamento é o inverso da codificação, conforme abordado nos próximos pontos.

Codificação

A codificação de Huffman é extremamente simples, assentando em poucos passos para a construção da árvore binária de símbolos, em que são aplicadas tabelas auxiliares (Huffman, 1952):

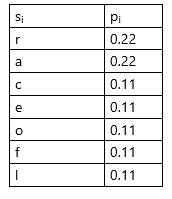
1. Ordenação dos símbolos (s_i) por ordem decrescente de probabilidade (p_i);

Tabela 1 – Exemplificação de uma tabela de símbolos (neste caso, caracteres) ordenados por ordem decrescente de probabilidades (para os valores obtidos, foi utilizado como fonte uma mensagem de texto constituída pela palavra “alforreca”, sendo os valores de probabilidades  correspondentes às frequências relativas de cada caracter na palavra)

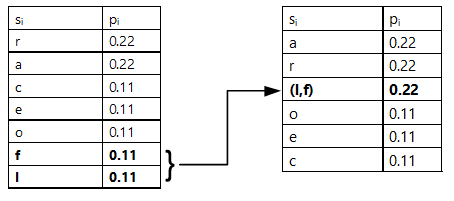
2. Contracção dos dois símbolos de menor probabilidade num símbolo hipotético cuja probabilidade será a soma       daqueles. O novo símbolo deverá ser posicionado na listagem decrescente;

 Esquema 1 – Exemplificação de 2º passo, com a contracção dos 2 símbolos de menor probabilidade num novo símbolo hipotético com a soma das probabilidades de ambos, sendo posteriormente integrado em nova tabela reordenada

3. Repetir o passo anterior até que todos os símbolos estejam agregados num único símbolo hipotético com probabilidade 1 (vide Esquema 2).

Estas tabelas auxiliares permitem a construção da árvore binária da raíz até às folhas, em que para tal se percorre as tabelas na ordem inversa da sua construção, i.e. começando na tabela final, que inclui todos os símbolos agregados numa probabilidade 1 (será a raíz) e passando por todas as restantes tabelas, em que cada nó – ou raíz de sub-árvore – representará um símbolo hipotético (agregação de vários símbolos, conforme obtido nos passos 2 e 3 referidos) e cada folha será um único símbolo.

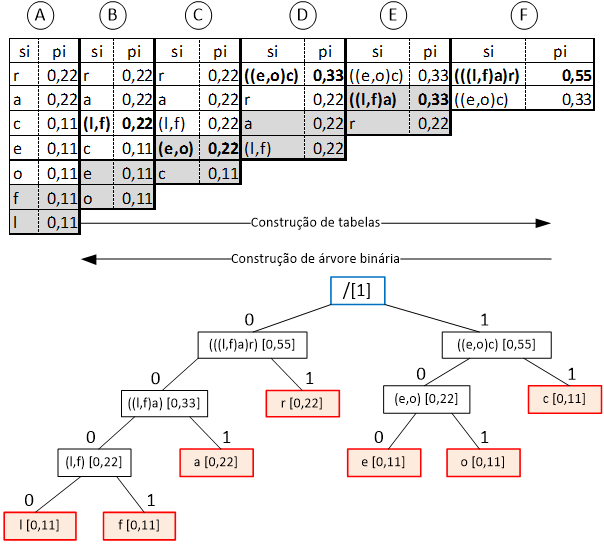
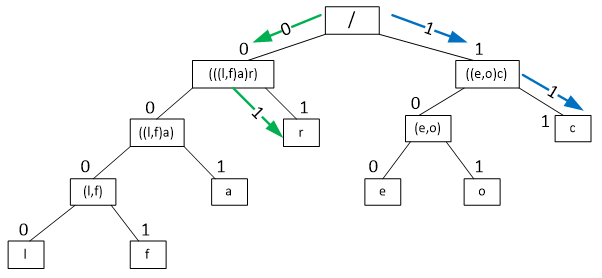
Esquema 2 – Exemplificação de construção sequencial de tabelas (ordenadas de A a F) e da subsequente construção de árvore binária, resultante da interpretação das tabelas de forma inversa (de F a A).

Nas tabelas, as células sombreadas evidenciam os símbolos que serão contraídos e cujo resultado será reordenado na tabela seguinte (novo símbolo agregado e probabilidade resultante marcados a negrito).

Note-se que, na árvore binária, os ramos esquerdos são identificados com 0 e os ramos direitos com 1 (Pu, 2006) (Li & Drew, 2004). As “folhas” (ou nós terminais, identificadas a vermelho) contêm os símbolos que pretendemos codificar. Em cada nó, temos representados os símbolos e a respectiva probabilidade (entre parêntesis rectos). A raíz (de probabilidade 1, pois “contém” todos os símbolos agregados) está identificada a azul.

Percorrendo a árvore da “raíz” até uma “folha”, obteremos o código correspondente ao símbolo presente nessa “folha”. Por exemplo, atentemos no símbolo “o”: percorrendo a árvore da raíz até à “folha” correspondente, navegaremos pelos ramos identificados com 1, 0 e 0, significando que s_i=”o” será codificado por 100. Usando o mesmo raciocínio, o s_i=”f” terá um código 0001.

Considerações sobre a codificação de Huffman

Saliente-se que, no exemplo supracitado, as probabilidades empregues no processamento foram obtidas por pré-processamento das frequências relativas de cada s_i. No entanto, e conforme referido anteriormente (vide capítulo “2. O algoritmo de Huffman”), essas probabilidades poderiam ser pré-determinadas antes da compressão. Esta diferenciação na ocorrência ou não de mapeamento de probabilidades será explorada na implementação programática do algoritmo de Huffman (vide capítulo “3. Implementação do Algoritmo de Huffman”).

O algoritmo de codificação de Huffman é extremamente simples e de aplicação directa, gerando códigos de comprimento variável (recorde-se que, por comprimento do código, referimos número de bits usados: o código 0001 tem comprimento de 4 bits), respeitando a entropia da informação: símbolos mais frequentes têm códigos de comprimento menor e símbolos com menor probabilidade de ocorrência têm comprimento superior.

A técnica de codificação de Huffman apresenta algumas propriedades importantes que, apesar de não serem demonstrarmos aqui, julgamos importante mencionar (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007):

• A primeira é denominada prefix-condition, sendo uma condição respeitada por todos os códigos gerados pelo algoritmo, i.e. nenhum código é prefixo de outro – esta condição é particularmente importante no processo de descodificação.
• Outra condição, desta feita enquadrada pela Teoria da Informação de Shannon (Shannon, 1948), é a limitação inferior pela entropia, ou seja, o número médio de bits resultante da codificação de Huffman nunca poderá ser inferior ao valor da entropia. De facto, Huffman satisfaz sempre a condição (Bashkaran & Konstantinides, 1997): (em que  representa o comprimento médio do código e H(S) o valor de entropia). O comprimento médio do código é apenas igual à entropia quando a probabilidade dos símbolos são potências de dois (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007).

Um dos aspectos interessantes da codificação de Huffman está na possibilidade de construção de diferentes árvores binárias (ou tabelas) para os mesmos dados de entrada. Esta situação é fácil de perceber se manipularmos o exemplo anterior (vide Esquema 2), pois poderíamos ter ordenado, na primeira tabela os símbolos (caracteres) “c”, “e”, “o”, “f” e “l” por ordem diferente – uma vez que comungam da mesma probabilidade, a sua ordenação na tabela pode ser realizada de forma aleatória – e por inerência a árvore resultante seria diferente. Da mesma forma, a disposição de símbolos na árvore pode ser realizada de forma distinta: no Esquema 2, os símbolos agregados “(((l,f)a)r)” e “((e,o)c)” poderiam ter sido dispostos nos ramos direito e esquerdo, respectivamente, por oposição à disposição “esquerda-direita” optada e, por conseguinte, a árvore teria uma configuração diferente e o código para cada símbolo iria ser também diferenciado.

No entanto, apesar da possibilidade de produção de árvores diferentes, é importante referir que todas elas são válidas, e respeitam integralmente os princípios definidos por David Huffman (Huffman, 1952). Este facto não representa problemas, na maior parte das situações, por duas razões:

– Em primeiro lugar, porque que o comprimento médio do código resultante das várias árvores possíveis é quase sempre semelhante (Blelloch, 2001);

– Não há problemas na descodificação, pois a árvore binária usada na descodificação terá de ser, obrigatoriamente, a mesma e única árvore criada durante a codificação;

Não obstante, este facto pode implicar que, de entre as árvores possíveis de construir com Huffman, os códigos resultantes possam implicar comprimentos de códigos por símbolo muito ou pouco variáveis. Como ilustração, atentemos no exemplo de (Blelloch, 2001):

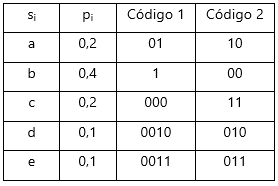
Tabela 2 – Para uma mesma mensagem com alfabeto {a, b, c, d, e}, existem 2 códigos de Huffman possíveis (Código 1 e Código 2), em que a variância por código no comprimento entre cada símbolo é diferente

Como podemos observar, para o código 1, temos símbolos com Código de 1 bit (eg.: “b” – 1) ou de 4 bits (eg: “d” – 0010) representando uma variância de 3 bits, enquanto que para o Código 2 essa variância é de apenas 1 bit (existe um máximo de 3 bits e um mínimo de 2 bits). Este facto, que é definido como “Variância mínima de Huffman” (Sayood, 2006), pode acarretar consequências apenas em algumas aplicações quando é importante reduzir o tamanho de buffers de transmissão/recepção ou manter débitos binários o mais constante possível (Blelloch, 2001), optando-se nesse caso pelo código com menor variância. Por norma, para obtenção do código de Huffman de menor variância, opta-se por, durante a construção das tabelas de símbolos ordenados por probabilidades, colocar os símbolos agregados o mais acima possível na lista – respeitando igualmente a ordenação decrescente por probabilidades (Sayood, 2006).

Descodificação

Para execução do algoritmo de descodificação de Huffman é peremptório que a árvore binária (ou uma tabela de mapeamento de símbolos e códigos) para todo o alfabeto de símbolos da mensagem esteja disponível no descodificador – geralmente, é incluída no cabeçalho do ficheiro comprimido (codificado). A partir desta árvore, o processo de descodificação é relativamente simples: basta percorrermos todos os nós mapeados pelo código, da “raíz” até ao símbolo respectivo (“folha”), bastando respeitar a norma de que um bit a 0 indica o ramo esquerdo e um bit a 1 aponta o ramo direito (Pu, 2006).

Esta é a aproximação directa quando se usa a descodificação bit a bit, em que o descodificador opera da seguinte forma (Salomon, 2007):

1)Obtém um bit dos dados comprimidos

2) Inicia a análise a partir da raíz da árvore binária:

– Se bit=0, “navega” para o próximo nó do ramo à esquerda

– Se bit=1, analisa o nó do ramo direito

3) – Se o nó é uma “folha”, então significa que o símbolo foi encontrado, retornando esse símbolo;

– Se o nó não é “folha”, obtém novo bit dos dados comprimidos e repete passo 2 para navegação para o nó inferior, reiterando a “navegação” bit a bit até chegar a uma “folha”

Sempre que é encontrado e retornado um símbolo (na prática, é encontrada uma “folha” da árvore), o novo bit obtido será analisado a partir da raíz, repetindo-se todo o processo até final de dados comprimidos de entrada.

Esquema 3 – Ilustração da sequência de navegação na árvore binária para a descodificação dos bits 0 e 1 (verde) e 1 e 1 (azul): imaginando que o descodificador recebe a sequência codificada 0111, será analisado o 1º bit que, sendo 0, indica ramo esquerdo (primeira seta verde); esse bit é descartado e analisado o 2º bit (1) que direcciona para o ramo direito (segunda seta verde) e subsequente folha com símbolo “r”; uma vez que foi encontrado e retornado um símbolo, o 3º bit será escrutinado a partir da raiz e, concomitantemente com o 4º bit, permite a descodificação de “c” (setas azuis)

Esta descodificação bit a bit, apesar de extremamente simples e de aplicação directa, pode não ser a mais apropriada quando é necessário obter débitos constantes de descodificação – como, por exemplo, na descodificação de dados em streaming. Este busílis é facilmente entendível se analisarmos o Esquema 3: se, para obtenção do símbolo “r” apenas é necessário descodificar 2 bits, para o símbolo “f” serão necessários 4 bits, portanto o tempo de execução dessa descodificação será inconstante entre símbolos. Para colmatar esta questão, pode ser empregue no algoritmo de Huffman um processo extra prévio à descodificação: a construção de uma tabela de mapeamento de símbolos por códigos de comprimento fixo, denominada Lookup Table ou LUT (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007).

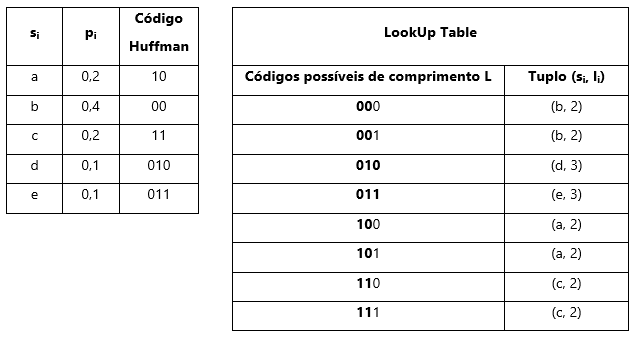
A tabela LUT é também uma tabela de mapeamento entre códigos e símbolos, com a diferença de que todos os códigos da tabela terão o mesmo comprimento. Por norma, esse comprimento em bits (que designamos L) corresponde ao comprimento do código mais longo e resultará numa LUT com 2^L entradas (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007). Atentemos na tabela seguinte, cuja LUT foi construída a partir de exemplo baseado em (Blelloch, 2001) – usando o código 2 (vide Tabela 2):

Tabela 3 – Exemplificação de LUT obtida a partir dos códigos de Huffman para uma mensagem com alfabeto {a, b, c, d, e} e probabilidades p_i.

Como verificamos, o maior código de Huffman por s_i existente tem 3 bits de comprimento (L=3). Como tal, a nossa Lookup Table terá 2³=8 entradas. Essas 8 entradas são correspondentes a todas as combinações binárias possíveis com 3 bits, conforme presente na coluna esquerda da LUT. Para os símbolos codificados com 3 bits (como “d” ou “e”), a correspondência é inequívoca, pois existe apenas uma combinação possível. No entanto, para os restantes símbolos, existirão mais possibilidades de códigos de comprimento L – pela lógica, verificamos que existem 2^L-li combinações possíveis para cada si de comprimento li (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007). De facto, se para s_i=”d” com l_i=3 existe 2^3-3=2⁰=1 código LUT (010), já para s_i=”a” com l_i=2 ocorrem 2^3-2=2¹=2 códigos possíveis na LUT (100 e 101). Na prática, durante a construção da LUT, são atribuídos ao símbolo s_i todos os códigos existentes para as combinações ^2L-li, pelo que, se existisse s_i=”n” cujo código de Huffman c_i=0, num alfabeto codificado com L=3, então na LUT ser-lhe-iam atribuídos os códigos 000, 001, 010 e 011 – correspondentes a todas as combinações possíveis para 0xx, representando x os dígitos 0 ou 1. Esta atribuição é realizada pela criação de um tuplo para cada entrada (coluna direita da LUT – Tabela 3), em que é atribuída a relação (s_i, l_i), ou seja, (símbolo, comprimento do código de Huffman).

Conforme supracitado, a construção da LUT é extremamente útil para situações em que é necessário realizar descodificação num débito constante – usando a LUT como referência, o descodificador pode analisar L bits a cada momento e para cada símbolo, ao invés de bits em série. Com efeito, utilizando a LUT o descodificador executa os seguintes passos:

1. Lê, do fluxo de dados codificado, L bits para um buffer. Recorde-se que L corresponde ao tamanho máximo (em bits) dos códigos da LUT ou o comprimento máximo do maior código de Huffman;
2. Corresponder ao código no buffer o símbolo respectivo a partir da referenciação pela LUT;
3. Utilizando o tuplo correspondente, o algoritmo descarta do buffer o número de bits equivalente ao l_i do s_i encontrado;
4. Nova leitura do fluxo de dados, inserindo no buffer os bits necessários ao seu preenchimento (tamanho L, logo se tiverem sido descartados l_i bits, serão carregados L-l_i bits);
5. Reiteração dos passos anteriores até final do fluxo de dados comprimidos/codificados.

Vejamos um exemplo simplificado, continuando com os elementos da Tabela 3:

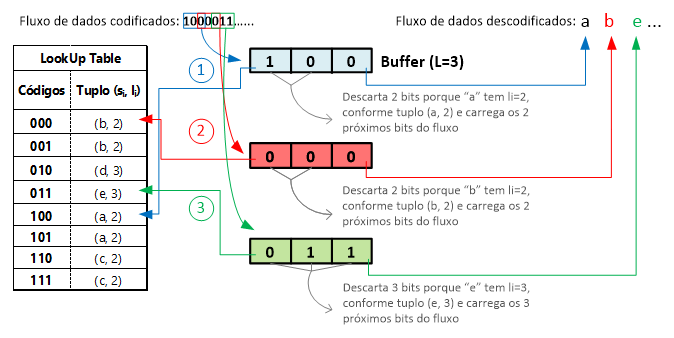
Esquema 4 – Exemplificação do funcionamento de descodificação de Huffman aplicada à utilização de uma LUT. Note-se como o algoritmo referencia o símbolo na LUT a partir dos bits carregados no buffer.

Como conseguimos aferir, a descodificação baseada em LUT torna-se muito mais fluida, permitindo um débito constante. Por outro lado, também é mais rápida que uma descodificação em série (Bashkaran & Konstantinides, 1997). Existem, no entanto, algumas restrições na utilização da descodificação baseada em LUT, como o caso de dados de imagem ou vídeo, cujo L é demasiado extenso para que a implementação da Lookup Table seja praticável devido a restrição espacial (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007).

Apenas como referência, existem diversas variantes de tabelas LUT (e.g. LUT hierárquicas) e ainda combinações de descodificação usando bits em série e tabelas LUT (Bashkaran & Konstantinides, 1997) (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007), no entanto estas técnicas não serão abordadas no presente documento.

Exemplo de aplicação

Para melhor ilustrarmos o modo de funcionamento do algoritmo de Huffman, iremos apresentar um exemplo prático e simples de codificação e descodificação. Para o efeito, vamos utilizar uma sequência de caracteres (texto): eeisieeiiieaaiiie. Por conseguinte, esta sequência – que representa a mensagem ou dados de entrada, não comprimidos – contém o alfabeto {a, e, i, s}, que representa o conjunto de símbolos a codificar.

Codificação

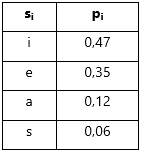
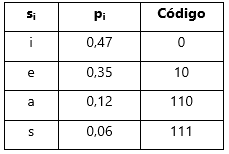
Passo 1 – Mapeamento de probabilidades. Neste exemplo, iremos utilizar como probabilidade (p_i) de cada símbolo (s_i) a frequência de ocorrência, calculando-se para o efeito a frequência relativa (número de ocorrências de s_i na mensagem dividido pelo número total de s_i), obtendo-se:

Tabela 4 – Modelo de probabilidades para a mensagem eeisieeiiieaaiiie

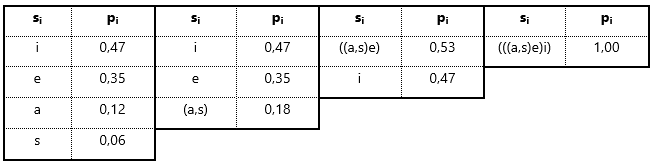
Passo 2 – Ordenação dos símbolos por ordem decrescente de probabilidades:

Tabela 5 – Tabela ordenada por ordem decrescente de probabilidades

Passo 3 – Agregar os dois símbolos de menor probabilidade num novo símbolo hipotético e reordenar os símbolos por ordem decrescente de probabilidades. Reiterar até obtermos um único símbolo de probabilidade 1:

Tabela 6 – Construção das tabelas de símbolos agregados até ao símbolo hipotético de probabilidade=1 (“raiz”)

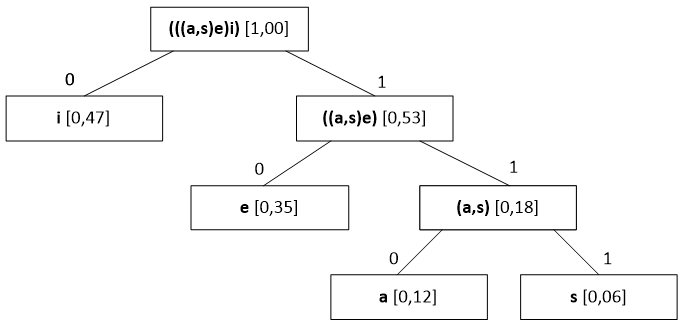
Passo 4 – Construção da árvore binária por interpretação das tabelas anteriores por ordem inversa e extrapolação do mapeamento de código por símbolo:

Esquema 5– Árvore binária resultante do algoritmo de Huffman aplicado à mensagem de exemplo

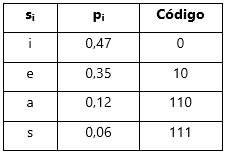
Tabela 7 – Mapeamento dos códigos por símbolo obtidos da árvore binária

Passo 5 – Codificação binária da mensagem, obtendo-se a mensagem codificada (comprimida), por codificação directa símbolo a símbolo, i.e., para a mensagem de exemplo, s₁=e, sendo que c₁=10, s₂=e -> c₂=10, s₃=i -> c₃=0, s₄=s -> c₄=111 até final da mensagem, resultando na saída de dados codificados 10 10 0 111… de tal forma que:

Dados de entrada (mensagem): eeisieeiiieaaiiie

Dados de saída (codificados/comprimidos): 10100111010100001011011000010

Descodificação

Vamos utilizar a sequência de bits resultante do exemplo de codificação como dados de entrada para descodificação (ou fluxo de dados comprimidos), fazendo a sua descodificação através de bits em série e por intermédio de LUT. Em ambos os casos, o ponto de partida é a árvore binária do algoritmo de codificação de Huffman, que permitirá quer a descodificação bit a bit, quer a construção da LUT. Como tal, a árvore (ou o mapeamento de símbolos-códigos) terá de ser disponibilizada ao descodificador.

Bits em série

Fluxo de dados de entrada (comprimidos/codificados):

10100111010100001011011000010

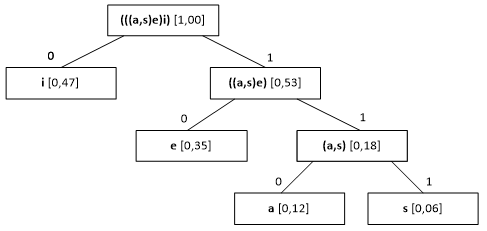
Árvore binária de Huffman (Esquema 5):

Passo 1 – Ler 1º bit (1) e navegar a árvore na direcção indicada (ramo direito)

Passo 2 – Como nó não é folha, ficar no mesmo nó, descartar bit anterior, ler próximo bit (0) e navegar para ramo esquerdo: atinge-se nó “folha”, correspondente ao símbolo “e”.

Passo 3 – Escrever o símbolo obtido no fluxo de dados de saída.

Passo 4 – Descartar bit anterior, ler próximo bit (1) e iniciar “navegação” da árvore a partir da “raíz”. Repetir os Passos 1 a 3 até final do fluxo de dados comprimidos.

Sintetizando, iremos obter, pela análise de cada bit, o segmento de texto descodificado:

Descodificação usando LUT

Fluxo de dados de entrada (comprimidos/codificados) e mapeamento de códigos:

10100111010100001011011000010

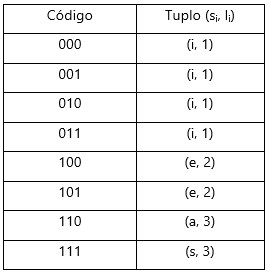
Passo 1 – Construção da LUT. Comprimento L=3, logo 2³=8 combinações possíveis. Preenchemos todas as combinações binárias possíveis com 3 bits e mapeamos o símbolo respectivo:

– Para s_i=i, c_i=0, pelo que todas as opções iniciadas por 0 lhe são atribuídas;

– Para s_i=e, c_i=10, pelo que todas as opções iniciadas por 10 lhe são atribuídas;

– Para s_i=a, c_i=110, pelo que a única opção 110 lhe é atribuída;

– Para s_i=s, c_i=111, pelo que a única opção 111 lhe é atribuída;

Adicionamos, à restante coluna, o tuplo de cada símbolo, emparelhando o l_i (número de bits usados na codificação de Huffman para o símbolo. Resulta, assim, a seguinte LUT:

Passo 2 – Criação de um buffer de tamanho L (3 bits) e inicialização da leitura do fluxo de dados comprimidos:

– Carregamento dos 3 primeiros bits (101) e referenciação desse código na LUT: refere-se ao tuplo (e, 2), pelo que escrevemos na saída o símbolo “e” e descartamos os 2 (é o comprimento em bits de “e”, conforme informação do tuplo) primeiros bits presentes no buffer;

– Ao bit (1) restante no buffer, adicionamos os dois próximos bits do fluxo de dados comprimidos (para que se preencham os L bits do buffer), obtendo 100: a partir da LUT, verificamos que corresponde a (e, 2), assim escrevemos o símbolo “e” na saída e descartamos os 2 primeiros bits do buffer;

– Repetimos todo o processo até final do fluxo de dados comprimidos;

De forma esquemática, este será o resultado da descodificação usando LUT:

Esquema 6 – Representação da descodificação usando um buffer e tabela LUT. Cada cor diferente representa cada preenchimento do buffer, extraíndo-se um símbolo (representando abaixo, com a mesma cor) e descartando os bits de tamanho li informados no tuplo

Implementação do algoritmo Huffman em java

Nos quadros abaixo são apresentados dois dos métodos utilizados para a implementação do algoritmo de Huffman.
No método “buildHuffmanRootString”, vai ser processada a tabela de frequências dos caracteres até que a mesma possua apenas uma entrada. No método “processarTabela”, a tabela vai ser percorrida até à última entrada e vai atribuir o bit 1 ao código binário dos caracteres presentes nesta, em seguida vai processar a entrada anterior e atribuir o bit 0 ao código binário dos caracteres presentes nesta. Posteriormente o símbolo da última entrada é concatenado ao símbolo da entrada actual e é eliminada a última entrada da tabela.

Shannon Fano e Huffman

Implementação do algoritmo Huffman em javascript

Como complemento deste artigo, foi implementado programaticamente o algoritmo de Huffman numa aplicação Javascript, objectivando a demonstração de todos os passos da codificação e da descodificação de forma simples e educativa.

A aplicação foi desenvolvida num simples editor de texto (Sublime Text 2), e encontra-se embebida numa página HTML – o objectivo final será a sua incorporação num website da instituição Universidade Fernando Pessoa, relativo à disciplina de Multimédia II, assim como a sua possível utilização demonstrativa pela docência.

Todas as linhas de código da aplicação foram construídas com base no princípio lógico do algoritmo de Huffman, sendo evidenciadas todas as estruturas de dados (tabelas de mapeamento de probabilidades, árvores binárias ou tabelas LUT) utilizadas nos passos de compressão/descompressão – respeitando o objectivo educacional da aplicação.

A referida aplicação baseia a sua execução na compressão de texto, pois torna mais simples a acepção do conceito de “conjunto de dados constituído por símbolos”. Esta está dividida em 2 secções principais: Codificador e Descodificador. Por seu turno, o Codificador está implementado de duas formas:

1. Huffman – Alfabeto – que permite ao utilizador a simples inserção de uma string (frase), havendo depois o mapeamento de probabilidades a partir das frequências relativas de caracteres;
2. Huffman – Inserção Manual – é solicitada ao utilizador a inserção dos caracteres individuais (alfabeto) intercalados com as respectivas probabilidades.

Para ambos os casos, serão apresentadas as tabelas de mapeamento de símbolos e probabilidades sequencialmente construídas de acordo com o algoritmo de Huffman.

O Descodificador apresenta igualmente duas opções:

1. Descodificador Série – sendo que o fluxo de dados comprimidos será analisado bit a bit.
2. Descodificador LUT – em que é construída uma tabela LUT que servirá para o processo de descodificação.
3. 

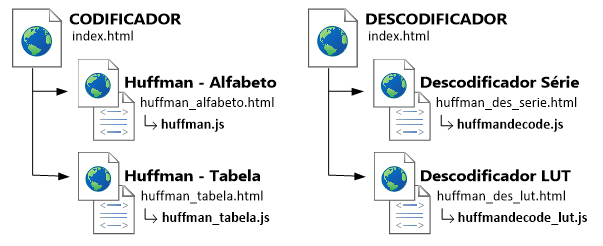
Esquema 7 – Ilustração da organização estrutural da aplicação

O código principal em Javascript que executa todo o processamento mimetizado de Huffman está alocado nos ficheiros .js integralmente transcritos no Anexo I.

Algoritmo codificação Huffman em javascript

Algoritmo descodificação Huffman em javascript

Desvantagens do algoritmo e comparação com outros métodos semelhantes

Durante mais de 25 anos, o algoritmo de Huffman afigurou-se como o mais eficaz método de compressão de entropia (Salomon, 2007), graças ao seu rácio de compressão por vezes próximo da entropia. Mesmo o algoritmo de Shannon-Fano – que apresenta uma lógica semelhante a Huffman, sendo a principal diferença a construção da árvore binária de cima para baixo (up-down) por oposição à abordagem bottom-up de Huffman – não consegue apresentar rácios melhores que o algoritmo de Huffman, além de apresentar dificuldades de implementação (Salomon, 2007) (Li & Drew, 2004).

No entanto, sempre foram reconhecidas algumas limitações ao algoritmo de codificação de Huffman. Uma das desvantagens já foi referida neste documento (vide “2.1.1 Considerações sobre a codificação de Huffman”), ou seja, a possibilidade de obtenção de mais que uma árvore binária – logo, códigos diferentes por símbolo – para os mesmos dados de entrada. Por seu lado, e também já supracitado, os melhores resultados (próximos da entropia) só se aplicam a quando as probabilidades dos símbolos são potências negativas de 2, ou seja, ,  etc.

Um dos problemas da codificação de Huffman referido por (Salomon, 2007) é a pouca tolerância a falhas na descodificação, isto é, caso ocorra uma simples falha na transmissão de um único bit dos códigos gerados pela codificação, toda a descodificação pode ser comprometida – este, contudo, um problema transversal a todos os métodos de codificação que produzem códigos variáveis (Salomon, 2007).

Mas, mais significativo ainda, como também referido em (Salomon, 2007), é o facto de o algoritmo de Huffman ser muito pouco eficiente quando aplicado a dados com alfabeto reduzido – embora se possa atenuar esta falha com a extensão do alfabeto manipulando grupos de símbolos (Blelloch, 2001).

Uma outra desvantagem que pode ser facilmente inferida, por ser decorrente da concepção do algoritmo, é a necessidade de ocorrer sempre um mapeamento de probabilidades prévio à codificação, seja por cálculo de frequências, seja por informação associada aos dados – ambos os casos poderão ser inconvenientes, seja pelo espaço extra necessário nos dados de entrada para informação das probabilidades “pré-concebidas”, seja pelo atraso temporal exigido pelo processamento de frequências dos símbolos (Salomon, 2007).

Por fim, o algoritmo de Huffman está sempre limitado ao mínimo de 1 bit por símbolo, pois o seu princípio de funcionamento implica a criação de um código para cada símbolo – rácios inferiores só seriam possíveis conjugando mais que um símbolo por código (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007).

Alguns destes inconvenientes são colmatados com abordagens diferentes ao algoritmo de Huffman, como o sejam extended Huffman – em que são codificados grupos de símbolos e não apenas símbolos individuais – ou adaptive Huffman – em que não é necessário o mapeamento inicial de probabilidades, mas as probabilidades e respectivas árvores binárias são reajustadas a cada novo símbolo lido durante a codificação – mas essas abordagens implicam uma complexidade deveras acrescida (Pu, 2006). Por conseguinte, o algoritmo de Huffman é, por vezes, preterido em benefício da codificação aritmética, sucedendo em algumas normas de codificação multimédia como o JPEG (Ribeiro & Torres, Tecnologias de Compressão Multimédia, 2007).

A codificação aritmética, cujas bases surgiram na década de 1960 e foi totalmente desenvolvida na década de 1970, tem também os seus princípios fundados no trabalho de Shannon e, por conseguinte, é também uma técnica de codificação baseada na entropia. Contudo, como o seu algoritmo permite que sejam ultrapassadas algumas das limitações de Huffman, já que, ao serem processados diversos símbolos num único código, rácios mais elevados são alcançados – é possível atingir menos de um bit por símbolo, mesmo em casos de alfabetos reduzidos (Salomon, 2007).

Não obstante, a codificação aritmética é alvo de patentes, além de um pouco mais complexa, o que torna a sua utilização ainda pouco apetecível, em função do algoritmo de Huffman, de código aberto e mais simples de implementar.

Conclusão

O algoritmo de codificação/descodificação de Huffman é extremamente simples, conforme foi possível analisar em todo este documento. De facto, é perfeitamente possível realizar manual e rapidamente todos os passos do algoritmo, quando utilizando dados de entrada de baixa complexidade, o que atesta a alocação de poucos recursos do algoritmo, mesmo para dados de maior complexidade. Não obstante esta simplicidade, o resultado da sua codificação é extremamente poderoso, permitindo rácios de compressão elevados sem qualquer tipo de perdas dos dados originais.

Por esta associação de grande simplicidade sem compromisso de uma elevada eficácia – e não obstante ter sido surgido há mais de 6 décadas – o algoritmo de Huffman continua a ser um dos codecs de maior importância nas tecnologias de informação. A sua relevância tem impacto quer em aplicações profissionais, quer no âmbito académico, onde continua a ser a base de estudos e investigação. No âmbito do multimédia, é um algoritmo fulcral, sendo parte integrante de normas largamente utilizadas e reconhecidas como o JPEG (imagem), MPEG (vídeo) ou MP3 (áudio).

Huffman tem, no entanto, algumas desvantagens (analisadas no ponto 4 deste documento) que, dependendo do contexto, poderão ser significativas, como o facto de ser ineficiente quando o alfabeto a codificar é de pequena dimensão ou o facto de ser necessária uma modelação de probabilidades prévia à codificação, que afecta a rapidez de processamento do algoritmo. Por essas desvantagens, o codec de Huffman é, por vezes preterido em função da codificação aritmética, dentro do modo dos codificadores sem perdas e categoria de compressão de entropia.

A elaboração deste artigo, coadjuvada com a implementação do codec de Huffman numa aplicação em Javascript, permitiu uma análise minuciosa de um dos algoritmos mais importantes do Séc. XX e de maior utilização em tecnologias actuais e profusas. A implementação permitiu uma visão prática, quer semântica, quer estrutural, dos conteúdos teóricos e a sua perfeita assimilação durante o processo de desenvolvimento.

Bibliografia

Bashkaran, V., & Konstantinides, K. (1997). Image and Video Compression Standards: Algorithms and Architectures. Norwell, MA: Kluwer Academic Publishers.

Blelloch, G. E. (2001). Introduction to Data Compression. In G. E. Blelloch, Algorithms in the Real World. Pittsburg, PA, United States of America: Carnegie Mellon University.

Huffman, D. A. (1952). A Method for the Construction of Minimum-Redundancy Codes. Proceedings of the I.R.E., 1098-1101.

Li, Z.-N., & Drew, M. S. (2004). Fundamentals of Multimedia. Upper Saddle River, NJ: Pearson – Prentice Hall.

Pu, I. M. (2006). Fundamental Data Compression. Oxford, United Kingdom: Elsevier.

Ribeiro, N. (2016). Apontamentos das Aulas. Multimédia II. Porto: Universidade Fernando Pessoa.

Ribeiro, N., & Torres, J. (2007). Tecnologias de Compressão Multimédia. FCA.

Salomon, D. (2007). Data Compression (4th ed.). London: Springer.

Sayood, K. (2006). Introduction to Data Compression. San Francisco: Morgan Kauffman.

Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379–423 & 623–656.

Wikimedia Foundation, Inc. (30 de 03 de 2016). Huffman Coding. Obtido em 02 de 04 de 2016, de Wikipedia, the free encyclopedia: https://en.wikipedia.org/wiki/Huffman_coding

Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.

Texto da autoria de Diogo Enes, Filipe Domingues,Tiago Mota Alão e revisto por Nuno Magalhães Ribeiro.

Código javascript da autoria de Diogo Enes, Filipe Domingues,Tiago Mota Alão.

Código java da autoria de António Vieira.

Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.