Introdução
O método de compressão que vai ser abordado neste artigo é o deflate, que combina o LZ77 com a codificação de Huffman.
LZ77 foi criado em 1977 por Abraham Lempel e Jacob Ziv, daí o surgimento do nome LZ (Lempel-Ziv). O LZ77 não tem patente registada, por isso é utilizado em muitos métodos de compressão. O algoritmo de Huffman foi desenvolvido por David Albert Huffman enquanto estudante do MIT, em 1952.
O método deflate foi originalmente definido por Philip Katz, como parte do formato de compressão de ficheiros ZIP, e mais tarde especificado no RCF em 1951.
É um popular método de compressão, originalmente utilizado nos formatos ZIP e GZIP, mas tem sido adoptado por diversas aplicações, destacando-se o protocolo HTTP, o formato de imagem PNG, ou o PDF.
O algoritmo LZ77 utiliza uma “janela deslizante” constituída pelo dicionário e pelo buffer, o dicionário contém os caracteres lidos e o buffer os novos caracteres. Essa janela vai sendo deslocada à medida que os símbolos vão sendo codificados, originando tuplas.
O método de Huffman é utilizado para comprimir as tuplas geradas pelo LZ77 para aumentar o rácio de compressão. Este algoritmo é um método de codificação estatística, que descobre a probabilidade de cada símbolo e vai juntando sucessivamente os dois símbolos com menor probabilidade. Com base nas estatísticas é construída uma árvore binária, possibilitando através da árvore obter-se os códigos binários para cada símbolo.
Justificação
Nos dias de hoje, e com o mundo direcionado para a internet, bem como a partilha de conteúdos multimédia, é fulcral a existência de algoritmos de compressão de dados eficientes. De modo a viabilizar a partilha desses conteúdos, sem sobrecarregar as redes.
Em termos de imagem, nos últimos anos ocorreu um grande salto tecnológico, a nível de rendering de imagem e de fotografia digital são necessários métodos de compressão eficientes e que acompanhem essa evolução nas tecnologias relacionadas com imagem.
Como o algoritmo deflate é utilizado no formato de imagem PNG, este artigo é bastante interessante para o aprofundamento dos conhecimentos acerca do mesmo.
Áreas de aplicação
O algoritmo deflate é uma combinação de diversas tecnologias de compressão de dados utilizado nos formatos ZIP ou GZIP, sendo o ZIP bastante popular e atualmente é usado na maioria das ferramentas de compressão de dados. O mesmo algoritmo também é utilizado para comprimir imagens no formato PNG.
O algoritmo do deflate
Codificação
LZ77
O algoritmo LZ77 original é constituído por dois componentes essenciais, uma janela deslizante de pesquisa, que se vai movendo ao longo do texto a codificar, e um buffer de pesquisa, que contém os caracteres imediatamente a seguir à janela.
Assim sendo, o algoritmo tenta encontrar a maior correspondência entre o texto presente na janela de pesquisa, e o texto presente no buffer. Escrevendo de seguida, no fluxo de dados comprimidos, tokens ou tuplas, constituídas pelo trio (deslocamento, tamanho, próximo símbolo).
O deslocamento corresponde à distância que a janela se moveu ao encontrar essa correspondência. Enquanto o tamanho representa o número de caracteres repetidos, e o próximo símbolo é o carácter seguinte na string a comprimir.
No deflate é aplicada uma versão modificada do LZ77, na qual o terceiro componente da tupla, o próximo carácter, é eliminado. Sendo que é escrito no fluxo comprimido o par (deslocamento, tamanho). Como o elemento próximo carácter era apenas utilizado nos casos em que não havia correspondência, mantê-lo presente nas tuplas acaba por ser desperdício. Sendo assim, quando não existe correspondência, o carácter não correspondido é escrito diretamente no fluxo comprimido.
Obtendo assim o fluxo comprimido resultante do algoritmo LZ77, que é constituído pelo par (deslocamento, tamanho) e pelos caracteres não correspondidos.
Algoritmo LZ77:
1) Leitura a partir dos caracteres de entrada até ao buffer estar cheio.
2) Verificação no dicionário, lendo da esquerda para a direita e pesquisa até encontrar correspondência. Caso exista mais que uma correspondência, então pegar na correspondência com maior sequência.
3) Se o comprimento for maior ou igual a 2, então escrever no ficheiro a tupla (distancia, comprimento, carácter), onde o carácter é o primeiro símbolo seguindo da sequencia correspondência.
4) Se não encontrar correspondência então escreve para o ficheiro a tupla (0,0,ASCII(c)).
Huffman
O algoritmo de Huffman é utilizado no deflate para comprimir as tuplas geradas pelo LZ77, aumento assim o rácio de compressão. A codificação de Huffamn é baseada em dicionários, ou tabelas. Assim sendo, no caso do deflate, possui duas tabelas, uma para os pares (deslocamento, tamanho) e outra para os caracteres literais não comprimidos.
Com base nessas tabelas, com os códigos dos tamanhos e as frequências dos caracteres são construídas duas árvores binárias. Uma para a tabela dos tamanhos e outra para os caracteres, obtendo-se os códigos binários para todas as tuplas e caracteres.
Os códigos finais são obtidos pela justaposição dos códigos da tupla e dos códigos para os caracteres literais.
Algoritmo Huffman:
1) Ordenar os símbolos de acordo com a respectiva frequência de ocorrência ou probabilidade.
2) Aplicar, de uma forma recursiva, um processo de contração aos dois símbolos com menor probabilidade, obtendo-se um novo símbolo hipotético igual á soma das probabilidades dos símbolos que lhe derem origem, repetindo-se esta contração até que todos os símbolos tenham sido contraídos num único símbolo hipotético com probabilidades igual a 1.
3) Usando os símbolos obtidos no parâmetro anterior, construir uma árvore binária de forma a obter um código único para cada símbolo.
Descodificação
Huffman
A descodificação é um método mais simples do que a codificação, bastando fazer o processo inverso.
Como os códigos finais são a justaposição dos códigos gerados por Huffman, na codificação, o código de cada uma das partes é obtido. Basta fazer a leitura da árvore de Huffman no sentido inverso, para obter o código correspondente ao tamanho de uma das tuplas e o carácter.
Posteriormente, é efectuada uma consulta às tabelas de Huffman para verificar o tamanho correspondente ao código, resultando dessa consulta as tuplas utilizadas pelo algoritmo LZ77.
Algoritmo Huffman:
1) Ler o fluxo de bits comprimido bit-após-bit, e percorrer a árvore a partir da raiz que se atinge uma folha.
2) Á medida que cada bit do fluxo comprimido é utilizado, deverá ser descartado. Quando atinge uma folha o descodificador de Huffman coloca na saída o símbolo correspondente a folha dá árvore, completando a descodificação do símbolo atual.
3) Repetir os passos 1 e 2 até que o fluxo comprimido tenha sido todo consumido.
LZ77
A descodificação do LZ77 no método deflate utiliza as tuplas descomprimidas a partir da descodificação de Huffman.
E é um processo bastante simples, basicamente é ler as tuplas e imprimir os caracteres, com as respectivas correspondências. Quando existe correspondência, a partir da distância determina-se a posição do carácter correspondente imprimindo a partir daí os caracteres, até que o total de caracteres seja igual ao comprimento, quando for igual imprime o carácter presenta na tupla.
Algoritmo LZ77:
Entrada: tupla recebida
Saída: sequência de símbolos
Enquanto o ficheiro não chegar ao fim
Ler o próxima tuple
Se a distancia for igual a 0 então imprime o carácter
Senão encontra a posição do carácter e imprime os caracteres até́ a
sequência terminar e imprime o carácter da tupla.
Exemplo de aplicação
Codificação utilizando o LZ77
Este exemplo demonstra a codificação utilizando o algoritmo LZ77, o algoritmo trabalha da esquerda para a direita, como podemos verificar a sequência “LSPSTRSA” já está codificada, faltando codificar “SAPPSTRPSTRO”.
Tamanho do dicionário: 6
Tamanho do buffer: 4
Tuplas criadas: (0,0,L), (0,0,S), (0,0,P), (0,0,T), (0,0,R), (0,0,A)
Percorre da esquerda para a direita até o limite máximo do dicionário até encontrar a correspondência, neste caso existe correspondência com a sequencia “SA”, começa na posição 6 do vector, logo a tupla vai conter (distância = [posição do primeiro carácter correspondente do buffer]-[posição encontrada no dicionário], comprimento, carácter), neste caso (2,2,P).
O buffer avança até à posição 11 (posição do buffer mínimo + comprimento + 1), e o dicionário também.
As próximas tuplas vão ser menores, neste caso encontram uma correspondência (1,1,S), porque a única sequência correspondente é só o carácter “P”, como se pode verificar temos “PSTR”, mas não utilizamos, porque o dicionário está limitado e a sequência “PST” já não se encontra dentro da sliding window, fazendo com que só houvesse aquela correspondência.
Nas próximas tuplas já não existe correspondência, porque dentro da janela limitada pelo dicionário não existe correspondência com os caracteres presentes no buffer ((0, 0, T) e (0, 0, R)).
Como se pode verificar, existem duas correspondências, uma onde o comprimento é 1 e outra onde o comprimento é, como se pretende a maior correspondência, então opta-se pela segunda sequência. Cada vez que é efectuada uma correspondência a slidding window avança uma posição, através de variáveis auxiliares, para de seguida percorrer todo o dicionário procurando uma correspondência melhor.
Encontrou uma correspondência, a sliding window avança. E o próximo caractere é analisado, é como se fosse uma sliding window auxiliar.
Ao passar para o próximo carácter este verifica que já não existe correspondência, logo a sliding window volta ao inicio para se analisar novamente o primeiro carácter do buffer. Este verifica uma correspondência com o carácter, a sliding window avança para o buffer conter novos elementos assim como o dicionário, que pode ajudar na codificação dos caracteres. Como se pode verificar a tupla vai ser a segunda sequência correspondente (4,4,O), o motivo pelo qual não incluirmos o O no comprimento é por ser o último caractere.
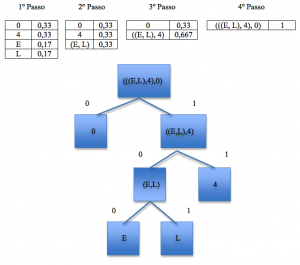
Codificação utilizando Huffman
O exemplo demonstra o funcionamento do algoritmo de Huffman, codificando duas tuplas geradas pelo LZ77.
Tuplas: (0, 0, R), (4, 4, O)
Descodificação utilizando o algoritmo de Huffman
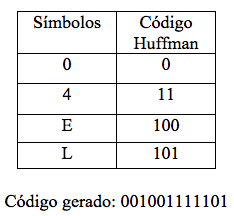
Para a descodificação utilizando o algoritmo de Huffman, o algoritmo recorre à árvore binária gerada na codificação, com o objectivo de descobrir quais os símbolos correspondentes aos bits gerados na coficação.
Código a descomprimir: 001 0 0 1 11 11 0 1
Código descomprimido: 0 0 E 4 4 L
No código de Huffman não existem códigos prefixos de outros. Para este algoritmo usamos uma variável auxiliar para percorrer a árvore binária. Como vemos no exemplo o primeiro bit do código a descomprimir é 0, logo a variável auxiliar toma o valor do filho esquerdo da raiz (se fosse 1 tomaria o valor do filho direito), como é um nodo folha encontramos o primeiro símbolo descomprimido, neste caso é o símbolo 0.
Volta-se á raiz da árvore e lê-se o próximo bit repetindo o processo até que os bits sejam todos descomprimidos.
Implementação do algoritmo deflate
Todo o código demonstrado a seguir foi desenvolvido na linguagem de programação Java.
Código LZ77
A codificação do LZ77 consiste em passar todos os caracteres do ficheiro para uma String, usando a concatenação e fazendo um cast para char no valor em ASCII do caractere lido no ficheiro.
Após a variável texto conter todo o texto lido do ficheiro, começa-se a percorrer a string com uma sliding window imaginária. Utilizámos várias variáveis auxiliares para nos ajudar na criação das tuplas. Enquanto o limite mínimo do buffer for menor do que o tamanho do texto, então este faz-se as comparações. Quando encontra uma correspondência e o min_buf é menor do que o tamanho do texto, é logo calculada a distancia, esta é armazenada numa variável auxiliar, a variável auxiliar do comprimento vai tomar sempre valor 0, para o caso de encontrar mais que uma correspondência, podendo assim comparar a melhor correspondência.
Dá-se inicio a um ciclo que verifica a maior sequência correspondente e enquanto a variável auxiliar que anda com a sliding window auxiliar para a frente for menor que o comprimento de texto (devido ao array começar do 0), então o comprimento auxiliar é incrementado e a sliding window auxiliar anda para frente, quando este não encontra mais caracteres correspondentes então compara o comprimento auxiliar com o comprimento, caso o comprimento seja menor, então atualiza-se a variável comprimento com o valor do comprimento auxiliar, e a variável distância também vai conter o valor da distância auxiliar.
Actualiza-se a sliding window, porque o caracter auxiliar que percorre posição a posição no dicionário ainda não chegou ao fim. Quando chega ao fim escreve-se para o ficheiro a tupla com a distancia, o comprimento e o próximo caractere que não tem correspondência. A sliding window é atualizada.
A descodificação é mais simples de fazer, a única coisa que se deve fazer é enquanto que a leitura não chegar ao fim, este lê do ficheiro para três variáveis.
A primeira leitura é feita para a variável dist, que contém a distancia, a segunda lê para uma variável o comprimento e por último é a leitura do caractere. Se a distancia for igual a 0, então concatena-se para uma variável texto o caractere vindo do ficheiro. Caso a distancia seja diferente de 0, então uma variável auxiliar vai conter a posição do primeiro caractere para copiar para a string texto, utilizámos uma variável auxiliar j, para percorrer desde a primeira posição até ao fim do comprimento, enquanto que o j for menor do que o comprimento, então concatena-se na string, os caracteres a partir da primeira posição, incrementando assim o i e o j. Ao fim de percorrer o ciclo while concatena-se o caractere armazenado na variável aux.
Código Huffman
Em primeiro lugar na codificação de Huffman tivemos de determinar a probabilidade de cada símbolo ocorrer no ficheiro lido. Cada símbolo é depois armazenado na primeira linha de uma matriz. A matriz vai servir para armazenar todos os passos de Huffman até termos uma probabilidade de 1.Isto é feito da seguinte maneira: a primeira linha da matriz vai ter N elementos (N = número de símbolos presentes no ficheiro) a segunda linha vai ter N-1 elementos já que vamos juntar em cada linha da matriz os dois elementos com menor probabilidade de ocorrer e assim sucessivamente. Na última linha da matriz apenas temos um elemento que é a soma de todos os símbolos, tendo probabilidade de 1. Este elemento vai servir de raiz para a árvore binária.
Como se pode perceber a construção da árvore binária vai ser feita usando os elementos da matriz, mas de baixo para cima, ou seja começamos pela última linha que vai conter a raiz da árvore, depois subimos uma linha e já vamos ter dois elementos em que um vai ser o filho esquerdo da matriz e outro o filho direito e assim sucessivamente até á primeira linha da matriz
Como já foi dito este método vai inserir os elementos da matriz de baixo para cima.
A parte mais complicada do trabalho foi passar para o ficheiro apenas os bits gerados pelos códigos de Huffman já que o Java apenas escreve bytes para ficheiros. A solução foi juntar os códigos gerados por Huffman em grupos de 8, de forma a não gastar-mos bits a mais na codificação, o problema aqui está que, a não ser que o número de bits seja múltiplo de 8, não vamos ter 8 bits para encher o último byte logo vamos ter de encher parte deste byte com 0’s.Sendo assim foi necessário no fim acrescentar outro byte para nos dizer quantos bits do byte anterior pertencem ao código gerado por Huffman.
A parte da descodificação acabou por ser bem mais fácil visto a parte mais complicado do código já estar realizada. Aqui o forma utilizado foi ler os bits do ficheiro comprimido por huffman para um buffer e utilizar a árvore binária gerada na codificação para chegar aos símbolos que correspondem a esses bits. Cada bit lido faz-nos percorrer a árvore binária (se lermos um 0 vamos para o filho esquerdo, se lermos um 1 vamos para o filho direito) quando chegamos a uma folha da árvore encontramos um símbolo, após isto voltamos á raiz da árvore e repetimos o processo até não existirem mais bits para ler.
Comparação com outros métodos semelhantes
Após a implementação do deflate testamos o desempenho do algoritmo com diversos ficheiros de texto, o resultado pareceu-nos satisfatório. Por exemplo para o ficheiro de texto: “trrtrtrtrrtrrtrtrtrrrtrrtrtrtrrtrrtrrtr”.
O rácio de compressão obtido é quase de 4:1, já que conseguimos comprimir um ficheiro de 39 bytes para um de 11 bytes. Ou seja para ficheiros com sequências repetitivas conseguimos ótimos resultados. Para um ficheiro de texto onde o texto passa por alguns parágrafos de um texto retirado de qualquer livro os resultados não são obviamente tão bons. Mesmo assim o rácio conseguido nestas situações anda geralmente entre 1,5:1 e 2:1.
Como se pode perceber o método deflate é mais eficiente quando temos sequências repetitivas em grande número.
Conclusão
O deflate proporciona bons rácios de compressão. A maior desvantagem deste algoritmo, é quando se quer comprimir ficheiros com poucas ou nenhumas repetições, isto porque na compressão vai se gastar quase tantos bytes como no ficheiro original. Já se tivermos ficheiros de texto com um grande número de repetições os resultados são bastante interessantes como se pode observar neste trabalho.
Bibliografia
- Salomon, D., “Data Compression”, Springer, 4th. Edition, 2007.
- Christina.Zeeh, “The Lempel Ziv Algorithm”, Janeiro 2003
- Ida Mengyi Pu, “Fundamental Data Compression”, 2006
- Morgan Kauffman, “Introduction to Data Compression”, 3rr Edition, 2006
- http://en.wikipedia.org/wiki/DEFLATE
- http://tools.ietf.org/html/rfc1951
- http://en.wikipedia.org/wiki/Huffman_coding
- http://en.wikipedia.org/wiki/LZ77_and_LZ78
- http://www.zlib.net/feldspar.html
Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.
Texto da autoria de José Pedro e revisto por Nuno Magalhães Ribeiro.
Código java da autoria de José Pedro.
Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.