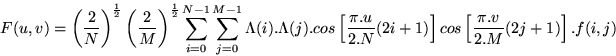(DCT da sigla em inglês para Discrete Cosine Transform)
Introdução
First used in 1974 (Ahmed, Natarajan and Rao).
Transformada Discreta de Cosseno é uma transformada relacionada com a transformada de Fourier, similar à Discrete Fourier Transform (DFT), mas que usa somente números reais. É a extensão da Transformada de cosseno ou Transformada contínua de cosseno para um domínio discreto e é muito utilizada em processamento digital de imagens e compressão de dados. Expressa uma sequência finita de pontos de dados em termos de uma soma de funções do cosseno oscilando em frequências diferentes.
DCT são importantes para inúmeras aplicações em ciência e engenharia, de compressão com perdas de áudio (por exemplo, MP3) e imagens (por exemplo, JPEG), onde pequenos componentes de alta frequência pode ser descartados, aos métodos espectrais para a solução numérica de equações diferenciais parciais. A utilização de cosseno em vez de funções seno é crítica para a compressão, uma vez que menos funções cosseno são necessários para aproximar um sinal típico, enquanto que para as equações diferenciais dos cossenos expressam uma escolha particular de condições de limite.
Existem cerca de 8 variantes standard da DCT, das quais 4 são bastante comuns. A mais comum e usada em tratamento de imagem é a type-II DCT, que é normalmente designada por “a DCT”; a sua inversa, a type-III DCT e designada por “iDCT” ou “a DCT inversa”.
Duas transformações relacionadas são: a transformada discreta do seno (DST), que é equivalente a uma DFT de funções reais e ímpares, e a transformada discreta do cosseno modificada (MDCT), que se baseia em uma DCT de dados sobrepostos.
O olho humano é mais sensível a mudanças no brilho do que a mudanças de cor, por isso, os dados da imagem são primeiro divididos numa componente de luminância e dois de crominância, e os componentes do ultimo são subamostrados relativamente à componente de luminância. A DCT reduz as componentes espaciais de altas-frequências da imagem, uma vez que o observador humano é mais sensível a erros de reconstrução de componentes de baixas frequências. Ou seja a DCT permite que os dados sejam representados em termos de coeficientes de frequência dos seus componentes. Como quase todas as imagens são compostas por informações de baixa frequência, os componentes de uma imagem, de frequência alta podem ser descartados.
Áreas de aplicação
A DCT, e em particular a DCT-II, é frequentemente usada em processamento de sinal e imagem, especialmente para a compressão de dados com perdas, porque tem uma propriedade forte “a compactação de energia”: a maior parte da informação do sinal tende a se concentrar em alguns componentes de baixa frequência da DCT.
A DCT é usada em JPEG compressão de imagem, MJPEG, MPEG, DV, Daala e compressão de vídeo Theora.
Também são amplamente utilizados na resolução de equações diferenciais parciais através de métodos espectrais, em que as diferentes variantes da DCT correspondem às condições limite par/ímpar ligeiramente diferentes para as duas extremidades da matriz.
O algoritmo da Transformada Discreta do Cosseno
Caso prático da compressão de um JPEG
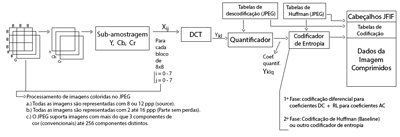
O algoritmo de compressão JPEG divide a matriz de luminância e as duas matrizes de crominância, que são as três matrizes que descrevem a imagem, em inúmeras matrizes, cada uma com o tamanho de 8 x 8 elementos. Com isto teremos varias matrizes compostas de 64 elementos, conhecidas como “sample values”. Sobre estas matrizes é aplicado o algoritmo DCT (Transformada discreta de cosseno), gerando outras matrizes, denominadas “Coeficientes de DCT”, cuja maioria dos elementos tem valor igual a zero. Esse processo translada a informação do domínio do espaço para o domínio da frequência.
A Transformada Discreta de Cosseno converte uma matriz de valores altamente correlacionados, e com uma distribuição de probabilidade uniforme, em um conjunto de valores menos correlacionados e com uma distribuição de probabilidade não uniforme. Em outras palavras, este algoritmo converte uma matriz numérica em outra, sendo que, a maior parte dos elementos desta nova matriz, especificamente os do canto inferior direito, tem valor igual a zero. O valor médio da matriz, que representa a cor fundamental dos 64 pixels, é chamado de componente DC (“Direct Current” – Corrente Direta), e está localizado no canto superior esquerdo da matriz de Coeficientes de DCT. Os outros coeficientes são denominados coeficientes AC (“Alternating Current” – Corrente Alternada) e representam os valores das pequenas variações de tonalidade e coloração do bloco.
Sabendo que os pixels de uma imagem tem correlação com seus vizinhos nas duas dimensões da imagem, e não apenas em uma dimensão, a transformada discreta de cosseno para ser usada na compressão de imagens também deve ser uma transformada bidimensional. A fórmula dessa transformada para uma matriz (ou seja uma imagem) p de tamanho N x M é:
e a correspondente transformada DCT inversa 2D é simplesmente F-1(u,v), exemplo:
Onde:
F(u, v) = coeficiente no domínio da transformada
u = eixo horizontal no domínio da transformada
v = eixo vertical no domínio da transformada
Λ(x) = 1 / √2 para x = 0
Λ(x) = 1 para x ≠ 0
x = u ou v
f(i, j) = amplitude no domínio do tempo
i = eixo horizontal no domínio do tempo
j = eixo vertical no domínio do tempo
Codificação
Transformada bidimensional DCT-II de NxN blocos são calculadas e os resultados são quantificados e codificados por entropia. Neste caso, N é tipicamente oito e a fórmula DCT-II é aplicada a cada fila e coluna do bloco. O resultado é uma matriz transformada de coeficientes de 8 × 8 em que o (0,0), elemento (superior esquerdo) é o componente DC (-frequência zero) e com o aumento da entrada de valores de índice verticais e horizontais representam frequências espaciais verticais e horizontais superiores.
Exemplo de aplicação
As operações básicas DCT são as seguintes:
– A imagem de entrada é N por M. – f(i,j) é a intensidade do pixel na linha i e na coluna j.
– F(u,v) é o coeficiente DCT na linha k1 e coluna k2 da matriz DCT.
– Para a maioria das imagens, grande parte da força do sinal encontram-se nas baixas frequências, estes aparecem no canto superior esquerdo da DCT.
– A compressão é alcançada quando os valores do canto inferior direito representam frequências altas, e são sempre pequenas o suficiente para ser desprezada, com pouca distorção visível.
– A DCT de entrada é uma matriz 8 por 8 de inteiros. Esta matriz contem a escala de cinzentos de cada pixel.
– Os pixels de 8 bits têm níveis que variam de 0 a 255.
Implementação do algoritmo DCT
Implementado em Javascript
Comparação com outros métodos semelhantes
A Transformada Discreta do cosseno são equivalentes a Fourier Transform (DFT) de aproximadamente duas vezes o comprimento, que opera em dados reais com simetria, em que em algumas variantes de entrada e/ou saída de dados são deslocados para metade de uma amostra.
Conclusão
O trabalho realizado foi extremamente interessante de realizar, apesar das dificuldades sentidas, dado que permitiu desenvolver a capacidade de desenvolvimento na linguagem de programação JavaScript e um maior conhecimento acerca do domínio abordado.
Bibliografia
[1] Discrete cosine transform [Em linha]. Disponível em
< http://en.wikipedia.org/wiki/Discrete_cosine_transform >
[Consultado em 15/05/2014]
[2] Transformada discreta de cosseno [Em linha]. Disponível em
< http://pt.wikipedia.org/wiki/Transformada_discreta_de_cosseno >
[Consultado em 15/05/2014]
[3] Joint Photographic Experts Group (JPEG) [Em linha]. Disponível em
< http://pt.wikipedia.org/wiki/JPEG >
[Consultado em 15/05/2014]
Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.
Texto da autoria de Antony Livera e revisto por Nuno Magalhães Ribeiro.
Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.