Introdução

As técnicas de compressão sem perdas garantem que os dados não sofrem alterações depois de descomprimido. No entanto, tem uma grande desvantagem em relação às técnicas de compressão com perdas que é a performance. Verificámos também que estão limitadas à entropia do código fonte e que raramente conseguem taxas de compressão 2:1 na maior parte das imagens. Para altas taxas de compressão utilizam-se as técnicas de compressão com perdas, de forma a que a imagem seja comprimida e, por isso, perca algum detalhe mas que este detalhe não seja perceptível ao olho humano. A principal diferença entre a compressão sem perdas e com perdas é o facto de a compressão com perdas estar assente em quantificadores.

O que é quantificação?

Quantificação é o processo de mapeamento de um conjunto contínuo de amostras num conjunto mais pequeno e finito de níveis de Output.

Os quantificadores têm vindo a desempenhar um papel cada vez mais importante no processamento de sinais. Foram feitos vários estudos nesta área. Um dos maiores problemas dos Engenheiros é a implementação de quantificadores com objectivo de performance.

Lloyd e Max propuseram independentemente um algoritmo que computasse quantificadores utilizando mean-square error distortion measure. Na actualidade este algoritmo é muito utilizado devido à facilidade da sua implementação.

Esta técnica foi desenvolvida independentemente por S. P. Lloyd em 1957 e J. Max em 1960. O desenvolvimento de Lloyd foi feito no departamento de pesquisa dos Laboratórios Bell.

Áreas de aplicação

Estes métodos de compressão são utilizados em áreas como a imagem, áudio e vídeo.

O algoritmo de Lloyd Max

O algoritmo de Lloyd Max promove uma redistribuição dos limites dos intervalos da amostra para representar os sinais.

Assim, a região do sinal que é mais densamente ocupada possuirá uma maior quantidade de amostras, enquanto regiões dispersamente ocupadas ficarão com poucas amostras.

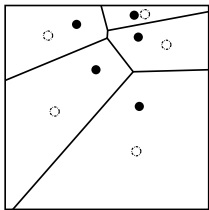
P.S: Diagrama de Voronoi, chamado centroidal, possui a propriedade da coincidência de coordenadas entre os pontos de geração de cada célula de Voronoi e o que indica seu centroide.

Por outras palavras, o algoritmo para criar o Diagrama de Voronoi, funciona da seguinte maneira:

• Conectar cada ponto amostral ao seu vizinho mais próximo, através de segmentos de reta;
• Construir bissectrizes, formando nos segmentos de rectas que conectam os pontos;
• Unir todas as bissectrizes nas rectas que conectam os pontos; e
• Unir rectas bissectrizes, formando o polígono que delimitam a área de influência de um ponto amostral.

Exemplo:

Codificação

Equações:

 Clique na imagem para aumentar

1. Escolha arbitrariamente um conjunto inicial {d1 <d2 < · · · <dL} com j = 1, . . . , L − 1.

2. Os centros de massa, equação (3.23), deste conjunto {xj} formam o {rj} inicial

3. Para 1 ≤ j ≤ L − 1, encontre dj com a equação (3.22).

4. Para 1 ≤ j ≤ L, encontre rj usando a equação (3.23)

5. Repita os Passos 3 e 4 até que a melhoria no MSE seja irrelevante, então pare.

Exemplo de aplicação

1. Processa o diagrama de Voronoi do conjunto de pontos actual;

2. Para cada célula do diagrama, calcula o seu centro de massa;

3. Desloca o ponto gerador para a posição do centro de massa encontrado na etapa anterior;

4. Verifica se o deslocamento médio dos pontos geradores do conjunto é minimamente aceitável para a aplicação, interrompendo o processo de refinamento caso o seja.

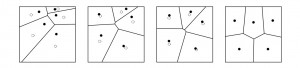 Clique na imagem para aumentar

Exemplo do algoritmo de Lloyd em quatro iterações diferentes. O diagrama de Voronoi do conjunto de pontos actuais em cada iteração é mostrado limitado por um quadrado.

Podemos verificar que os pontos do conjunto representado por pontos preenchidos vão de encontro aos pontos sem preenchimento que são os centroides.

Implementação do algoritmo Max Lloyd

Para verificar de que forma é tratada uma imagem pode fazer o download do aplicativo.

Pseudo-código:

Início

Escolher conjunto inicial de níveis de quantificação r0

i = 0

repetir

calcular dj utilizando a equação (3.22)

i = i + 1

calcular rj utilizando a equação (3.23)

até que |rj – rj| < E

Comparação com outros métodos semelhantes

A compressão através de Max Lloyd consegue ter melhores resultados a nível de detalhe que as técnicas de quantificação escalares uniformes.

Podemos fazer essa constatação nas imagens abaixo:

Clique na imagem para aumentar

Podemos também verificar que Max Lloyd tem mais uma escala cinza mais definida:

Clique na imagem para aumentar

Conclusão

A elaboração deste trabalho foi bastante interessante pois, além de me permitir entender como os dados são processados, também me permitiu aprofundar os meus conhecimentos em JAVA.

Bibliografia

Salomon, D., “Data Compression”, Springer, 4^th. Edition, 2002.

Ribeiro, Nuno e Torres, José, Tecnologias de Compressão Multimédia, 1ª edição, FCA – Editora de Informática, Porto, 2009.

September 26, 2010, Author: Martin Mayer Quantization of Images and Lloyd‘s Algorithm

http://www.cpdee.ufmg.br/~renato/TesesEDissertacoesOrientadas/Dissertacao-LucasPantuzaAmorim.PDF

Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.

Texto da autoria de Filipe Gois e revisto por Nuno Magalhães Ribeiro.

Código java da autoria de Filipe Gois.

Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.