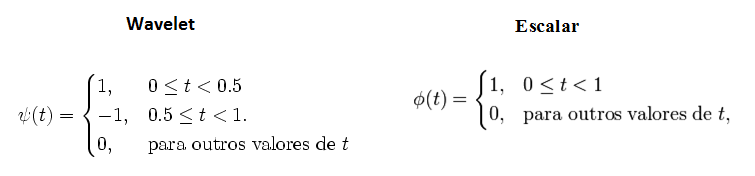Introdução

As wavelets são ferramentas matemáticas para decompor funções hierarquicamente. De um modo geral, permitem descrever através de uma função, desde o detalhe mais genérico ao mais específico. Independentemente da função corresponder a uma imagem, uma curva, uma superfície, ou um sinal, as wavelets oferecem uma técnica elegante para representar os níveis de pormenor (Stollnitz, DeRose & Salesin, 1995).

A aplicação da transformada wavelets tem-se destacado em vários domínios como a engenharia, a física, a matemática entre outros. Uma aplicação muito referenciada é a compressão de imagens utilizada no Federal Bureau of Investigation (FBI), para impressões digitais. Assim com a aplicação das wavelets o problema referente ao armazenamento de dados devido ao tamanho da informação foi resolvido. Cada impressão digital passou a ocupar um espaço de armazenamento menor, através do rácio de compressão em uma proporção de 20:1 (Graps, 1995).

No presente artigo aborda-se a transformada Haar, devido à sua simplicidade e ao fato de ser utilizada em variadas aplicações, em particular no processamento de imagens digitais.

Inicialmente aborda-se a transformada de Fourier, seguida da caracterização da wavelet e apresenta-se uma breve descrição da análise em multirresolução. No ponto seguinte é efetuada a sistematização da transformada Haar, é abordada a sua aplicação às imagens, e caracteriza-se a wavelet unidimensional e bidimensional. O último ponto é referente ao código fonte utilizado para a implementação das wavelets.

Transformada de Fourier

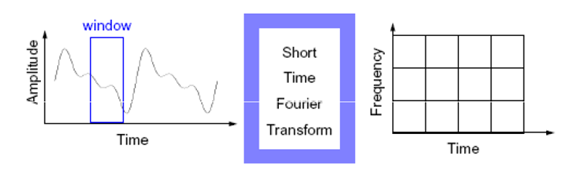
A transformada de Fourier é uma técnica principal utilizada no processamento de sinais e tem como objetivo a transformação de um sinal (função) do domínio do espaço para o domínio de frequência (Gonzalez & Woods, 1992). Tendo em consideração que a transformada de Fourier não relaciona os intervalos de tempo com as frequências aponta-se o problema relacionado com o fato de considerar o sinal (função) todo. Ou seja, é apropriada para sinais estacionários.

De acordo com o mencionado anteriormente e tendo em consideração que a maioria dos sinais são transitórios ou não estacionários, Dennis Gabor adaptou a transformada de Fourier de modo a analisar uma pequena porção do sinal em deterioramento do sinal todo. Assim passa a ser chamada de transformada por janela de Fourier. Esta, considera uma janela que se desloca pelo sinal e avalia cada um separadamente. O problema apontado prende-se com o tamanho da janela, uma vez definido é constante para todas as frequências.

Wavelet

O conceito de wavelet foi apresentado pela primeira vez em 1909 por Haar, e continua a demonstrar a sua utilidade em diversas áreas como análise de imagem, processamento de sinais, entre outros.

As wavelets são ferramentas matemáticas para decompor funções hierarquicamente. De um modo geral, permitem descrever através de uma função, desde o detalhe mais genérico ao mais específico. Independentemente da função corresponder a uma imagem, uma curva, uma superfície, ou um sinal, as wavelets oferecem uma técnica elegante para representar os níveis de pormenor (Stollnitz, DeRose & Salesin, 1995).

A análise da wavelet tem como objetivo “ver a floresta e as árvores” (Graps, 1995; como citado em Lima, 2002, p.14). Uma vez que se apresentam com características muito próprias, utilizaram-se em compressão de imagem e sons, em processamento de geometria digital, em problemas de computação gráfica, na medicina, na biologia, entre outros. (Lima, 2002).

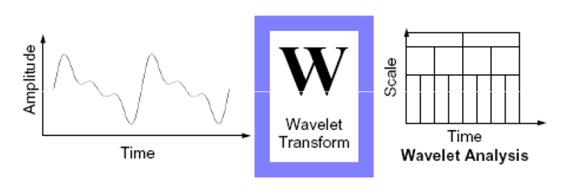
As wavelets diferem da transformada de Fourier uma vez que permitem, para além de obter informação do domínio da frequência, também obtém informação do domínio do tempo.

Análise Multirresolução

O conceito da análise multirresolução foi criada por Mallat e Meyer em 1986, permitindo assim a construção de novas bases de wavelets. A decomposição multirresolução proporciona a interpretação invariante de escala da imagem, esta interpretação não deve mudar quando a escala da imagem é alterada. O conceito de espaço vetorial da álgebra linear permite uma melhor compreensão deste método. Especificamente o espaço vetorial V pode designar-se como um grupo de objetos (vetores) para os quais a adição e o produto escalar estão definidos (Mallat, 1989).

Transformada Haar

A transformada de Haar é considerada a mais simples das wavelets e são computacionalmente as menos exigentes, em súmula permite obter médias e diferenças de uma sequência de valores reais originando assim, uma nova sequência formada pelas médias e diferenças da sequência inicial. Possibilita também, através da repetição deste processo criar uma análise multirresolução da sequência original (Ribeiro & Torres, 2009).

Para a obtenção de médias e diferenças referidas anteriormente, aplica-se a função de escalamento e a função wavelet ao longo do sinal de entrada. Especificamente, a função de escalamento utiliza-se para a obtenção das médias e a função wavelet para obter as diferenças, como ilustram as funções apresentadas (Ribeiro & Torres, 2009).

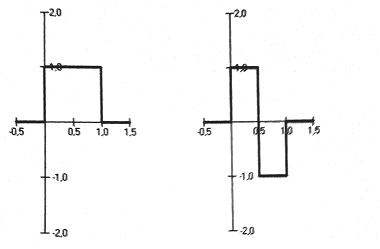
 Graficamente a função de escalamento é conhecida como função retangular, tal como consta na figura a seguir (lado esquerdo). Do lado direito da mesma figura mostra-se a função wavelet.

Transformada Wavelet aplicada às imagens

Em análise à figura apresentada abaixo pode-se observar os processos de compressão e descompressão aplicados a imagens digitais. Ao nível da perda de informação verifica-se que esta ocorre na aplicação da transformada wavelet, bem como na etapa de quantificação dos coeficientes transformados. Os codificadores de entropia permitem a compressão sem que haja a perda de informações.

 Diagrama em blocos do processo de compressão/descompressão de imagens (retirado de Sanches, 2003).

“A transformada wavelet direta mapeia os dados da imagem original para um outro domínio, sem fornecer nenhuma compressão dos dados em relação a imagem original, porém a transformada inversa, em muitos casos, permite uma reconstrução exata das informações anteriores. Neste novo domínio os dados são caracterizados por uma grande quantidade de valores iguais ou próximos de zero, que torna eficiente o uso de codificadores de entropia. A compressão é realizada pela quantização/limiar e pela codificação dos coeficientes wavelets. A reconstrução da imagem é efetuada invertendo as operações do processo de compressão” (Sanches, 2003, p.15).

2.3.1 Wavelet Haar – Unidimensional (1D)

De acordo com Stollnitz, DeRose e Salesin (1995) e de modo a compreender como funcionam as wavelets começa-se por dar um simples exemplo. Assumindo que temos uma imagem a 1D com uma resolução de 4 pixéis com os seguintes valores:

[  9  7  3  5  ]

Podemos representar esta imagem utilizando a base da transformada wavelet. Para implementar este processo, aplica-se a média dos primeiros pixéis pares, para obter a nova imagem de resolução mais baixa, assumindo os seguintes valores:

[  8  4  ]

Claramente, alguma informação foi perdida neste processo de cálculo da média. Para recuperar os quatro valores dos pixéis originais dos dois valores médios precisamos armazenar alguns coeficientes detalhe, que permitem recuperar a falta de informação. Neste caso, escolhe-se 1 para o intervalo entre 7 e 9, e -1 para os valores fora deste intervalo. Executando estas etapas recursivamente obtêm-se os seguintes valores:

De seguida é definida a transformada wavelet dos quatro pixéis originais, de modo a ser o único coeficiente que representa a média global da imagem original, seguido pelos coeficientes de detalhe em ordem crescente de resolução. Assim, para a base Haar unidimensional, a transformada wavelet da imagem original de quatro pixéis é dada por:

[  6  2  1  -1  ]

A transformada wavelet foi calculada de modo recursivo através da média e da diferenciação de coeficientes, a qual se chama banco de filtros. Este processo será mencionado no ponto referente ás wavelets bidimensionais (2D). De mencionar que nenhuma informação foi perdida ou ganha no presente processo. Ainda, de referir que a imagem pode ser reconstruida em qualquer resolução através do processo recursivo.

Wavelet Haar – Bidimensional (2D)

Para decompor uma imagem bidimensional podem ser utilizadas as wavelets de decomposição padrão e não padrão (Stollnitz, DeRose & Salesin, 1995).

Na decomposição padrão começa-se por aplicar a transformada wavelet unidimensional, fornecendo o coeficiente de média e os coeficientes de detalhe para cada uma das linhas da imagem, este processo é aplicado de forma recursiva. O resultado deste processo são todos os coeficientes de detalhe, com a exceção do primeiro pixel que corresponde ao único coeficiente médio. Assim, aplicação da transformada é utilizada até se obter o menor nível de resolução possível (Sanches, 2003).

De modo a compreender o processo de decomposição padrão apresenta-se o exemplo a seguir:
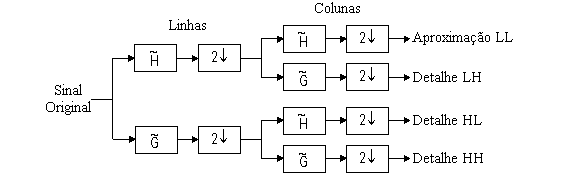
Uma dada imagem (m, n) é filtrada na direção m (linhas) originando uma imagem passa-baixo (L) e uma imagem passa-alto (H). Assim, obtém-se as imagens diminuídas a metade em relação à imagem original. O próximo passo é referente à filtragem na direção n (colunas) obtendo quatro subimagens:

• LL (passa-baixo, passa-baixo) correspondendo a banda passa-baixo em ambas as direções.
• LH (passa-baixo, passa-alto) correspondendo a banda passa-baixo na direção vertical e passa-alto na direção horizontal.
• HL (passa-alto, passa-baixo) correspondendo a banda passa-alto na direção vertical e passa-baixo na direção horizontal.
• HH (passa-alto, passa-alto) correspondendo a banda passa-alto em ambas as direções.

Transformada discreta wavelet bidimensional (retirado de Sanches, 2003).

Através da aplicação da transformada wavelet obtém-se uma imagem com o mesmo tamanho, no entanto esta é composta por três imagens de detalhe (HL, LH e HH), e uma imagem de aproximação (LL). Todas as imagens obtidas possuem metade da resolução da imagem original. Este processo pode ser repetido na subimagem LL, de onde resultam mais quatro subimagens, e assim sucessivamente até obter um único coeficiente de aproximação.

Em relação ao algoritmo da transformada wavelet inversa é aplicado de forma similar, mas no processo inverso.

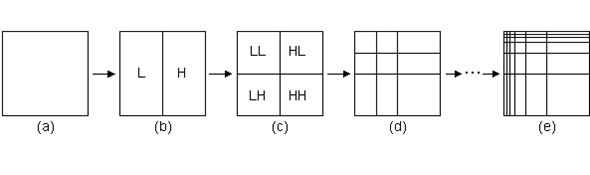
Estágios de decomposição wavelet bidimensional padrão com 5 níveis de resolução (retirado de Sanches, 2003).

Como exemplo do processo mencionado mostra-se a aplicação da transformada à imagem Lenna.

Decomposição padrão da imagem Lenna (retirado de Sanches, 2003).

Outro tipo de transformada wavelet bidimensional é a decomposição não padrão, caracterizada por alternar entre os cálculos nas linhas e nas colunas. Inicialmente calcula-se as médias e as diferenças do valor dos pixéis de cada linha da imagem, seguindo-se o cálculo das médias e das diferenças em cada coluna. De modo a ilustrar o que foi dito apresenta-se a imagem a seguir.

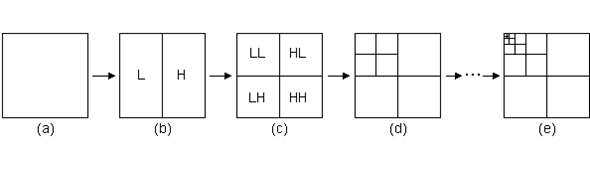
Estágios de decomposição wavelet bidimensional não padrão (retirado de Sanches, 2003).

Em análise à imagem mencionada anteriormente, e especificamente a que corresponde à figura (c) verifica-se que é composta por quatro imagens menores. A imagem do canto superior esquerdo contém os coeficientes de baixa resolução, correspondente à média dos pixéis da imagem original. Nas restantes imagens os coeficientes correspondentes são os de alta resolução, que permitirão a reconstrução da imagem. A transformação será completa com a repetição deste processo recursivamente, apenas nos quadrantes que contem as médias em ambas as direções.

Tal como no exemplo referente á decomposição padrão, recorre-se á imagem Lenna para mostrar a aplicação da decomposição wavelet não padrão.

Decomposição não padrão da imagem Lenna (retirado de Sanches, 2003).

Na decomposição wavelet padrão as operações ocorrem apenas em uma dimensão, ou seja, começa-se por se aplicar a transformada apenas nas linhas e depois nas colunas da imagem. Este processo torna a computação da decomposição não padrão mais eficiente.

Após a análise da decomposição, a transformada wavelet permite também armazenar uma imagem em várias resoluções, como apresentado na figura a seguir. “Dessa maneira, podemos transmitir inicialmente os coeficientes da imagem com menor resolução, permitindo assim a visualização de uma aproximação da imagem. Com isso, é possível efetuar a reconstrução gradual da imagem pelo recetor. Em seguida, somente a informação necessária para derivar uma versão mais detalhada da imagem, a partir da imagem de mais baixa resolução, é transmitida. Após a transmissão de todos os coeficientes detalhe, o recetor terá uma cópia completa da imagem. Este tipo de transmissão é conhecido como transmissão progressiva (progressive transmission). Para a transmissão progressiva os coeficientes wavelet precisam ser arranjados em ordem de importância. A decomposição em multirresolução da transformada torna-se ideal para isso” (Sanches, 2003, p.20).

Imagem Lenna em várias resoluções (retirado de Sanches, 2003).

A reconstrução gradual da imagem Lenna pode observar-se na figura abaixo. A reconstrução da imagem é feita a partir dos coeficientes de aproximação do nível quatro de decomposição (a), os coeficientes de detalhe também do nível quatro permite a visualização da imagem (b). A imagem (c) é referente à reconstrução a partir dos coeficientes detalhe de nível três. Em relação à imagem (d) a reconstrução é efetuada a partir do nível dois de decomposição, e por último, a imagem (e) corresponde à imagem original reconstruída.

Reconstrução progressiva a partir da imagem com menor resolução (retirado de Sanches, 2003).

Código fonte dos algoritmos da transformada wavelet Haar

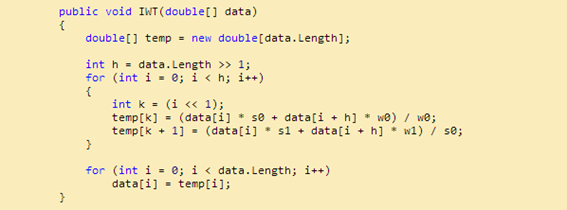
Transformada Wavelet Haar 1D

Transformada Wavelet Haar 2D

Transformada Wavelet Haar inversa 1D

Transformada Wavelet Haar inversa 2D

Referencias Bibliográficas

Bantikyan, H. (2013). Codeproject.com. Acedido em 1 de Abril de 2014 www.codeproject.com/Articles/683663/Discrete-Haar-Wavelet-Transformation

Graps, A. (1995). An introduction to wavelets. IEEE Computational science & engineering, 2(2), 50-61.

Gonzalez, R. & Woods, R. (1992). Digital image processing. EUA: Prentice Hall

Lima, P. (2002). Wavelets: Uma introdução. Matemática Universitária, 33, 13-44.

Ribeiro, N. & Torres, J. (2009). Tecnologias de compressão multimédia. Lisboa: FCA.

Mallat, S. (1989). A theory for multiresolution signal decomposition: The wavelet representation. IEEE Transactions on pattern analysis and machine intelligence, 2(7), 674-693.

Stollnitz, E., DeRose, T. & Salesin, D. (1995). Wavelets for computer graphics: A primer part 1. IEEE Computer graphics and applications, 15(3), 76-84.

Sanches, I. (2003). Compressão sem perdas de projeções de tomografia computadorizada usando a transformada wavelet. Retirado de www.dainf.ct.utfpr.edu.br/~ionildo/wavelet/