Introdução

A codificação de Huffman, é um tipo de codificação que atribui um código de bits de comprimentos variável a cada símbolo, onde os símbolos com menos probabilidade tem um código de bits de comprimento maior relativamente aos símbolos que têm maior probabilidade, tendo este menor comprimento, tornando assim a codificação de Huffman umas das codificações mais eficientes, tendo também como principais vantagens os seguintes pontos:

• Ser uma codificação relativamente rápido e de acesso aleatório, pois a sua árvore é construída durante a compressão/descompressão (não necessitando de ser enviada previamente);
• Não necessita de conhecer a estatística dos símbolos fonte;
• Se a estatística variar, o código adapta-se automaticamente.

Este algoritmo foi desenvolvido independentemente por Faller (1973) e Gallager (1978), sendo melhorado por Knuth (1985), ficando assim conhecido como algoritmo FGK. Existe ainda outro melhoramento concebidos por Vitter (1987), ficando conhecido por algoritmo V, o qual não ira ser apresentado aqui.

O número total de bits transmitidos numa sequência de comprimento t com n símbolos diferentes encontra-se limitado ao intervalo S­n+1 a 2S+t­4n+2, sendo S o número de bits usado pelo algoritmo de Huffman.

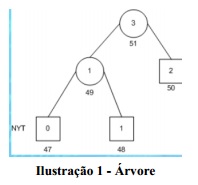
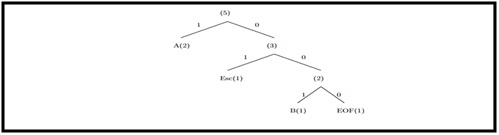
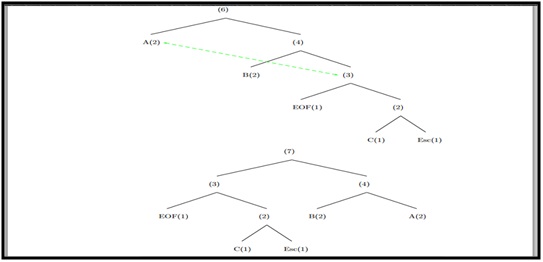
A codificação de Huffman Adaptativa pode ser descrita na forma de uma árvore binária, similar a que se encontra na figura abaixo (ilustração 1).

Áreas de aplicação

Uma variante do código de Huffman é a Codificação de Huffman Adaptativo ou Huffman Adaptativo (dinâmica). Essa técnica foi criada para que se pudesse usar a compressão de Huffman em casos onde nos quais não se conhecem as frequências de ocorrência de cada caracter no texto.

Neste caso, devemos actualizar constantemente todas as frequências (entrada) na árvore. Quando um caracter a ser codificado já existe na árvore ele é codificado de acordo com a sequência de bits especificada. Quando um caracter é novo, ele é enviado sem compressão para o destino. O codificador então actualiza a sua árvore para que seja incrementado o contador de ocorrências do caracter ou criada uma nova entrada na árvore. Este método é utilizado em aplicações que envolvem transmissão de texto.

O algoritmo do “Huffman Adaptativo”

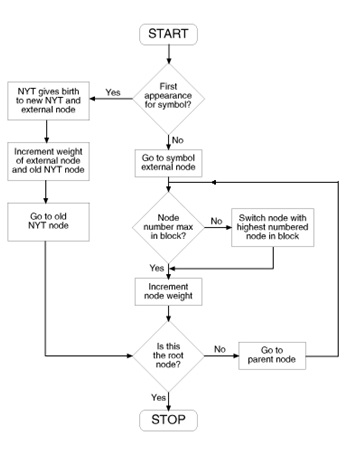
A principal ideia para o funcionamento de este algoritmo é que a árvore de Huffman dever ser inicializada vazia, ou seja, é inicializada com um único nó conhecido como o ainda-não-transmissíveis (NYT) ou código de escape, indo esta sendo modificada e actualizada com os símbolos que se encontram a ser lidos e processados ​​(no caso do compressor, o termo “processamento” significa comprimido e, no caso de o descompressor, isso significa descomprimido).

O compressor e o “descompressor” devem modificar a árvore, da mesma forma, por isso, em qualquer ponto do processo, eles devem usar os mesmos códigos, embora esses códigos possam vir a ser alterados a cada passo do processamento. Dizemos que o compressor e descompressor são sincronizados, ou que trabalham em sincronia (embora não precisem necessariamente de trabalhar juntos, pois a compressão e descompressão normalmente ocorrem em momentos diferentes), sendo a descodificação um espelho das operações do codificador.

Codificação

Inicialmente, o compressor começa com uma árvore de Huffman vazio, onde na qual não existem símbolos nem códigos atribuídos ainda, sendo assim inicializada com um único nó, conhecido como ainda não-transmissíveis (NYT) ou código de escape., sendo este código enviado de cada vez que um novo caracter que não está na árvore é encontrado, seguido pela codificação ASCII do carácter.

O primeiro símbolo a ser recebido é simplesmente escrito na saída, na forma descompactada, sendo o símbolo então adicionado à árvore e ao qual lhe é atribuído um código. Isso permite assim ao descompressor distinguir entre um novo código e outro já existente. Além disso, o procedimento cria um novo nó para o novo caracter e um novo NYT a partir do nó de NYT. Sempre que um novo símbolo de entrada símbolo já existente na árvore é encontrado, o seu código actual é escrito na saída, e a sua frequência é incrementada.

Uma vez que esta modifica a árvore, esta é examinado de modo a verificar se ainda é uma árvore de Huffman (melhores códigos), se não for a melhor árvore, esta e recalculada e modificada de modo a podermos ter sempre a melhor árvore de Huffman, uma operação que resulta em códigos modificados.

A fim de por este algoritmo para trabalhar, precisamos adicionar algumas informações adicionais para a árvore de Huffman. Em adição a cada nó com um peso, será atribuído um número de nó único. Além disso, todos os nós que têm o mesmo peso, são considerados no mesmo bloco, sendo esses números de nós atribuídos de tal forma que:

1. Um nó com um peso superior ira ter um número de no mais elevado;
2. Um nó pai sempre terá um número de nó mais elevado do que o dos seus nós filhos.

O algoritmo de actualização que é utilizado, simplesmente nós dá a certeza que a árvore é sempre a melhor árvore possível, e que a propriedade é mantida, com tudo o nó raiz terá sempre o maior número de no, pois é o que tem maior peso.

Descodificação

O descompressor espelha os mesmos passos. Quando se lê a forma descompactada de um símbolo, ele adiciona à árvore e atribui-lhe um código. Quando se lê um código comprimido, ele verifica a árvore actual para determinar o símbolo do código a que pertence, e incrementa a frequência do símbolo e reorganiza a árvore da mesma forma como o compressor.

Trata-se imediatamente claro que o descompressor precisa saber se o item tem de entrada apenas é um símbolo descompactado (normalmente, um código ASCII de 8 bits) ou um código de comprimento variável. Para eliminar qualquer ambiguidade, cada símbolo descompactado é precedido por um código de escape especial, de tamanho variável.

Quando o descompressor lê esse código, sabe que os próximos oito bits são o código ASCII de um símbolo que aparece no arquivo compactado pela primeira vez.

O problema é que o código de escape não deve ser de qualquer dos códigos de comprimento variável utilizado para os símbolos. Estes códigos são, contudo, modificados de cada vez que a árvore é reorganizada, razão pela qual o código de escape também deve ser modificado. Uma maneira natural de fazer este objectivo é adicionar uma folha em branco para a árvore, uma folha com uma frequência zero de ocorrência, que é sempre atribuído ao 0 – galho da árvore. Uma vez que a folha está na árvore, é atribuído um código de comprimento variável. Este código é o código de escape antes de cada descompactação do símbolo. Como a árvore está a ser reorganizada, a posição do vazio da folha e assim, a sua mudança de código, mas este código de escape é sempre utilizado para identificar os símbolos não comprimidas em o arquivo compactado.

Exemplo de aplicação

Neste método é usado um símbolo especial que é colocado na árvore logo na altura da inicialização, que é o caracter cujo vai para o ficheiro indicar que o caracter está a ocorrer pela primeira vez. A seguir a este código aparece sempre o novo caracter. Com esta informação o descodificador conseguirá gerar a mesma árvore do codificador. As árvores de huffman têm de obedecer sempre á seguinte propriedade: se visitarmos a árvore por nível, da esquerda para a direita e de baixo para cima, as frequências estarão sempre ordenadas de forma não descendente. Assim, símbolos com altas frequências terão códigos mais pequenos. O requerimento de em cada nível as frequências estejam ordenadas da esquerda para a direita serve apenas para simplificar a actualização da árvore.

• Vamos considerar o NYT como o caracter especial
  • Se o caracter é novo:
    • Colocar o código do nyt no ficheiro comprimido seguido do novo caracter;
    • Inserir na árvore sempre o mais abaixo e á esquerda possível (se é novo deverá ficar no local com menor frequência).
  • Se o caracter (X) já existe na árvore.
    • Colocar o código do caracter no ficheiro comprimido;
  • Actualizar a árvore:
    • Comparar o peso do caracter X que estamos a codificar (F) com o sucessor na árvore (da esquerda para a direita e de baixo para cima). Se este tiver frequência F +1 ou superior os nodos continuam ordenados e não é necessário alterar nada. Senão, algum sucessor de X tem frequência idêntica a F ou inferior. Neste caso, X deve ser trocado com o último do grupo (excepto X não deve ser trocado com o seu pai).
      • Incrementar a frequência de X de F para F+1. Incrementar as frequências de todos os seus pais.
      • Se X for a raiz pára, senão repetir com o pai do nodo como X.

Codificação

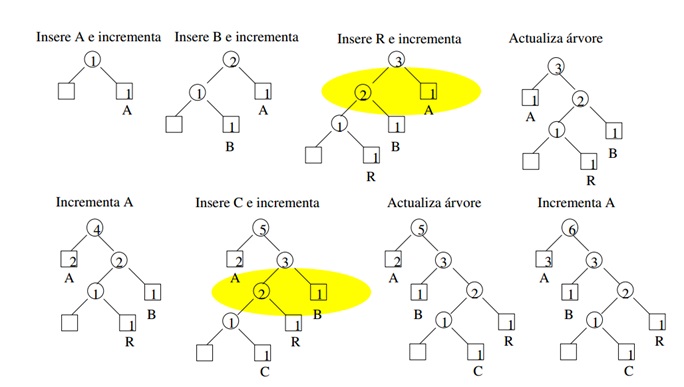
Exemplo de uma codificação onde vamos codificar “AABBC”.

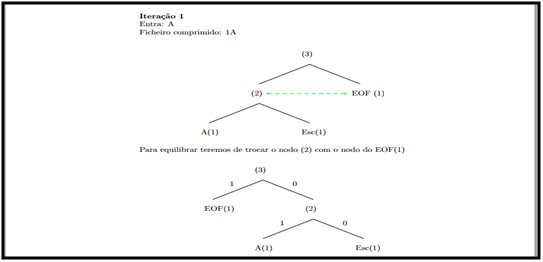
Iteração 1:

Nesta primeira iteração teremos de trocar o nodo (2) com o nodo do EOF (1), o que entrou foi o “a” e o ficheiro comprimido foi “1a”.

Ilustração 2 – Iteração número um.

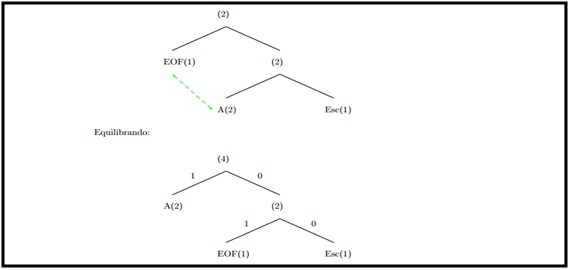
Iteração 2:

Na segunda iteração Entra: A e o Ficheiro comprimido: 1A01, atualizando-a.

Ilustração 3- Iteração número 2.

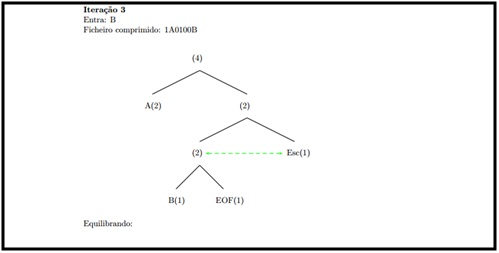
Iteração 3:

Caracter de entrada “B” ficheiro comprimido “1A0100B”.

Ilustração 4 – Iteração número 3.

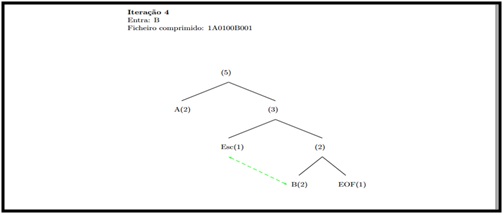
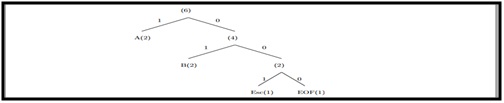
Iteração 4:

Caracter de entrada “B”, ficheiro comprimido “1A0100b001”.

Ilustração 5 – Iteração número 4.

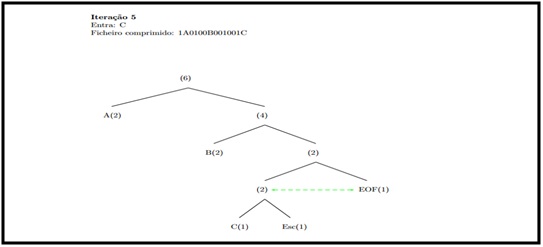
Iteração 5:

Caracter de entrada “C”, ficheiro comprimido final “1ª0100B001001C”.

Ilustração 6 -Iteração número 5.

Descodificação

O descodificador “espelha” os mesmos passos. Quando lê um código comprimido, usa a árvore corrente para descodificar o símbolo, e atualiza a árvore da mesma forma utilizada pelo compressor

A diferença principal é que o descodificador precisa saber se o código a ser descodificado é um símbolo descomprimido (normalmente, um código ASCII de 8 bits) ou um código de tamanho variável. Para remover qualquer ambiguidade, cada símbolo descomprimido é precedido por um código de escape de tamanho variável. Quando o descodificador lê este código, ele sabe que os próximos 8 bits são o código ASCII do símbolo que aparece no arquivo comprimido pela primeira vez. O problema é que o escape não pode ser nenhum dos códigos variáveis utilizados pelos símbolos. Já que estes códigos estão sendo modificados cada vez que a árvore é reconstruída. Uma forma de resolver esse problema é adicionar uma folha vazia a árvore, uma folha com frequência zero de ocorrência, que é sempre fixada como um branch vazio da árvore. Como a folha está na árvore, ele possui então um código associado a ele. Este código é o código de escape precedendo todo símbolo descomprimido no arquivo comprimido. De acordo com a reconstrução da árvore, a posição da folha vazia pode ser modificado, mas o código de escape é sempre utilizado para identificar símbolos descomprimidos no arquivo comprimido.

Na descodificação a quantidade de bytes necessários para representar o tamanho original do arquivo e o tamanho original do arquivo são lidos. Logo após o processo de descodificação inicia-se lendo o arquivo bit a bit reconstruindo a árvore de Huffman sempre que necessário e estimando as probabilidades associadas e tratando o caso especial da ocorrência do código do escape. Quando o número total de bytes for atingido a descodificação é abortada e o restante do arquivo é ignorado.

Implementação do algoritmo

Exemplo: “ABRACADABRA”

Código: “A 0 B 00 R 0 100 C 0 1100 D 0 110 110 0”

A árvore de Huffman é inicializada com um único nó, conhecido como o ainda-não-transmissíveis (NYT) ou código de escape. Este código será enviado de cada vez que um novo caracter que não está na árvore, é encontrado, seguido pela codificação ASCII do carácter. Isso permite ao descompressor distinguir entre um novo código e outro já existente. Além disso, o procedimento cria um novo nó para o novo caracter e um novo NYT a partir do nó de NYT. Sempre que um caracter que já está na árvore é encontrada, o código é enviado o peso aumenta.

A fim de por este algoritmo a trabalhar, precisamos adicionar algumas informações adicionais para a árvore de Huffman. Em adição a cada nó com um peso, será atribuído um número de nó único. Além disso, todos os nós que têm o mesmo peso, são considerados no mesmo bloco.

Ilustração 8 – Explicação do algoritmo.

Comparação com outros métodos semelhantes

1. Vantagens sobre o huffman:

• A árvore é construída durante a compressão/descompressão (não necessita de ser enviada previamente);
• Não necessita de conhecer a estatística da fonte;
• Se a estatística variar, o código adaptar-se automaticamente.

2. Algoritmo (pontos chave):

• Reservar um símbolo de “escape” na árvore para representar os símbolos que ainda não ocorreram;
• Actualizar os pesos de todos os nós da árvore com o respectivo número de ocorrências (permite obter a estatística da fonte);
• Actualizar a árvore de forma a que todos os nós têm pesos ordenados da esquerda para a direita e de baixo para cima  (árvore de Huffman).

Conclusão

A ideia-chave é a construção de uma árvore de Huffman adaptativo que é ideal para a parte da mensagem, e reorganizá-lo, quando necessário, para manter a sua optimização.

O desenvolvimento deste projecto de multimédia foi uma tarefa bastante motivadora. Por um lado, porque permitiu a aplicação dos novos conhecimentos adquiridos, não só na formação realizada na aula de multimédia II mas também ao longo da licenciatura de Engenharia Informática.

As limitações deste trabalho é a parte gráfica, pelo que o grande problema que ocorreu foi desenhar na parte gráfica a árvore binária, e de que forma fosse vindo caracteres e os correspondestes pesos eles iam actualizando na árvore binária.

Na parte de implementação do programa está bem estruturado dividido em funções, dividir para conquistar. Porém poderá ser melhorado no aspecto de organização do código mas principalmente na parte gráfica.

Bibliografia

1-      Apontamentos do professor.

2-      Applet Funcionamento programa. Disponível em < http://www.cs.sfu.ca/CourseCentral/365/li/squeeze/AdaptiveHuff.html>.

4-      Huffman Adaptativo [Em linha]. Disponível em < http://en.wikipedia.org/wiki/Adaptive_Huffman_coding>.

5-      Compressão e codificação de dados. Disponível em < http://revistas.ua.pt/index.php/revdeti/article/viewFile/1668/1546>.

6-      Compressão e codificação de dados. Disponível em < http://www.di.ubi.pt/~palmeida/tecnologias_multimedia/Sebenta.pdf>.

Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.

Texto da autoria de Alessandro Miguez (27583) e Ana de Sousa (25681) e revisto por Nuno Magalhães Ribeiro.

Código java da autoria de Alessandro Miguez (27583) e Ana de Sousa (25681).

Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.