Introdução

Existem dois modos de comprimir a informação, usando Técnicas de compressão com perdas ou Técnicas de compressão sem perdas. Esta última que também é conhecida por lossless compression, bit-preserving ou reversible compression. Como o próprio nome indica nas técnicas de compressão que se enquadram neste modo não existe perda de informação entre os dados originais e os dados que serão primeiramente comprimidos e depois “descomprimidos” , ou seja, o fluxo de dados de entrada é idêntico ao fluxo de dados de saída e é nesta ultima categoria que se enquadra a codificação Aritmética.

O ideia de Codificação aritmética foi proposta pela primeira vez por Peter Elias no início dos anos 60  e foi descrita por Abramson em 1963 pela primeira vez. Por sua vez as primeiras demonstrações práticas deste método só foram feitas por  Rissanen  em 1976, Pasco em 1976 e Rubin em 1979. Witten em 1987 e Moffat  em 1998 discutiram os princípios e os detalhes da implementação da codificação aritmética mostrando também exemplos.

A codificação aritmética enquadra-se no grupo de técnicas de codificação de entropia, que é um termo genérico que se refere às técnicas de compressão e codificação que não têm em conta a natureza da informação a ser comprimida, ou seja, este tipo de compressão ignora a semântica da informação a ser comprimida sendo representada por sequências de bits.

Ao contrário da Codificação de Huffman que gera um novo código para cada símbolo de entrada na Codificação Aritmética atribui-se um único código a cada conjunto de dados (ficheiro de entrada ou outro tipo de conjunto de dados).

Justificação

A cada dia que passa o crescimento da qualidade presente nos formatos de áudio, vídeo e imagem e por esse motivo o consequente aumento no espaço de armazenamento que estes ocupam é cada vez mais importante a existência de algoritmos de compressão sendo o crescimento da partilha de conteúdos multimédia principalmente do streaming de vídeo através da Internet. É necessário a utilização de técnicas de compressão que permitam a transmissão dos mesmos sem perdas significativas de qualidade uma vez que seria impossível transmitir estes formatos sem compressão, pois a estrutura da rede de internet existente nos dias de hoje não suporta a transmissão destes conteúdos sem compressão de uma forma eficiente e rápida.

Áreas de aplicação

Como a técnica de codificação aritmética é uma técnica patenteada o seu uso em aplicações fica limitado pelo fator monetário daí que muitas vezes deixa de ser viável a sua utilização em projetos open-source e em vez desta seja usada em seu detrimento a técnica de codificação de Huffman, ainda que esta seja menos eficiente que a codificação aritmética pode ser usada em projetos open-source e software de baixo custo.

Alguns exemplos de aplicações da técnica de codificação aritmética:

• “bzip2” – Software de compressão open-source (versão anterior);
• Codificadores e descodificadores do formato de ficheiros JPEG;
• O codec H.264/AVC usa a codificaçao aritmética;

O algoritmo da codificação Aritmética

O algoritmo de codificação Aritmética faz parte das técnicas de codificação de entropia por isso, não tem em conta a semântica do fluxo de entrada/saída dos dados codificados/descodificados, codificando o fluxo de entrada num único código. O código resultante é visto como um sub intervalo aberto no limite superior do intervalo ( [0, 1[ ).

Como acontece no algoritmo de codificação de Huffman os conjuntos de dados mais prováveis correspondem a sub intervalos mais amplos gerando assim menos bits de precisão

Codificação

Para podermos proceder a codificação de um fluxo de entrada de dados é necessária a existência de um alfabeto com a probabilidade de ocorrência de cada símbolo nele contido. O fluxo de dados de entrada no início do processo encontra-se no intervalo  [0, 1], este intervalo vai ser dividido em sub intervalos que correspondem a cada um dos símbolos do alfabeto da seguinte forma:

• O limite inferior(fechado ( [ ) ) é a probabilidade cumulativa até, mas deixando de fora o símbolo;
• O limite superior(aberto ( [ )  ) de cada subintervalo cumulativa até incluindo o símbolo;

O primeiro passo do codificador Aritmético consiste na leitura e processamento do primeiro símbolo do fluxo de dados de entrada, em seguida vai detetar o sub intervalo correspondente ao símbolo lido e fazer com que este seja o novo intervalo atual que por sua vez vai fazer com que os restantes símbolos do alfabeto sejam recalculados com os novos limites do intervalo.

Para calcular para cada símbolo do fluxo de entrada aplica-se o algoritmo da codificação Aritmética abaixo apresentado:

 Fig 1. Algoritmo de codificação aritmética

No final do processamento vai ser usado o sub intervalo calculado apartir do último símbolo do fluxo de dados de entrada e o codificador Aritmético vai determinar um código aritmético contido nesse intervalo.

Aqui está uma aproximação do algoritmo que o codificador aritmético usa para a geração de um código binário ótimo, em que o high é o valor do sub intervalo superior e o low o valor do sub intervalo inferior do último símbolo calculado presente no fluxo de entrada.

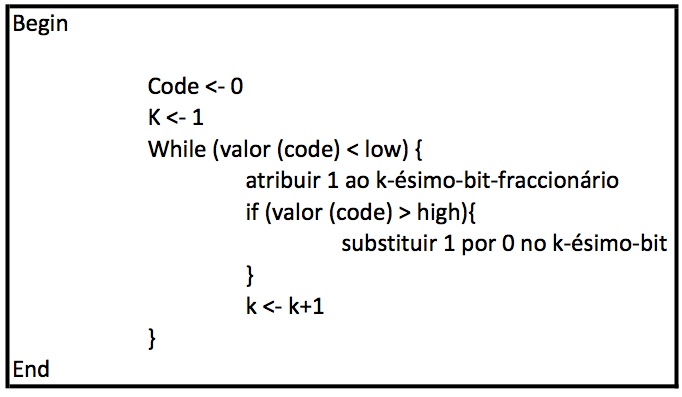Fig 2. Algoritmo de Geração do código binário ótimo

Descodificação

O descodificador aritmético usa o código binário produzido pelo codificador aritmético que representa a totalidade dos dados comprimidos.

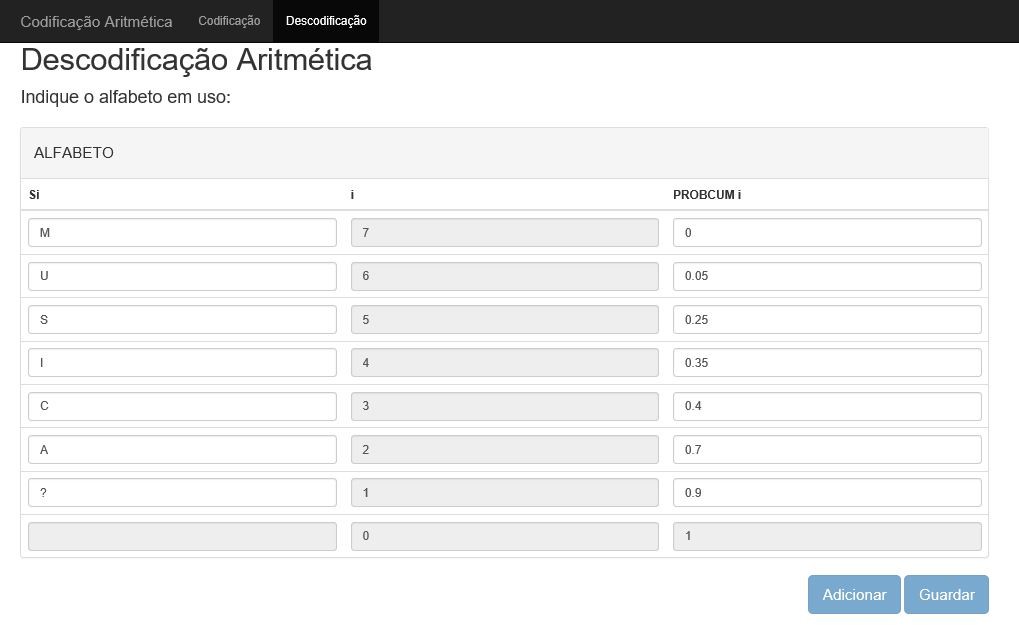
No inicio do processo de descodificação o descodificador atribui a cada símbolo do alfabeto um índice único (i) ao qual associa um probabilidade cumulativa, depois desse processo o descodificador vai aplicar o algoritmo a seguir apresentado:

Fig 3. Algoritmo de descodificação aritmética

 Exemplo da Aplicação

Codificação

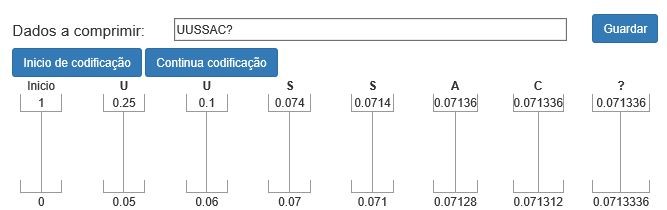
Usando o algoritmo de codificação aritmética para codificar por exemplo a mensagem “UUSSAC?”.

O primeiro processo que o codificador executa consiste no processamento do primeiro símbolo da mensagem “UUSSAC?”, ou seja, o símbolo “U” e vai procurar na tabela abaixo apresentada o sub intervalo correspondente a esse símbolo, que vai ser o intervalo atual usado pelo codificador, sendo necessário calcular os intervalos dos restantes símbolos do alfabeto.

Figure 4 Largura dos sub intervalos dos símbolos para o exemplo apresentado

Codificando o símbolo “U” o intervalo atual corresponde agora ao intervalo [0,05 ; 0,25[, sendo fácil de observar que o subintervalo_alto corresponde a 0,25 e o subintervalo_baixo corresponde a 0,05.

Os intervalos superior e inferior do símbolo seguinte da mensagem são calculados através expressões presentes no algoritmo de codificação aritmética:

Novo limite superior = 0,05 + (0,25 – 0,05) x 0,25= 0,10

Novo limite inferior = 0,05 + (0,25 – 0,05) x 0,05= 0,06

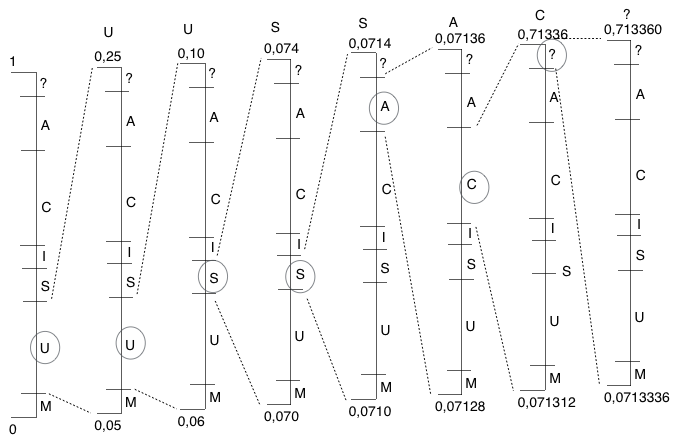Fig. 5 Exemplo de codificação da mensagem

Estes cálculos devem ser efetuados sucessivamente aplicando o algoritmo de codificação aritmética até chegar ao último símbolo cujos sub intervalos calculados vão ser os limites superiores e inferiores do código binário que vai ser calculado pelo algoritmo apresentado na figura 2.

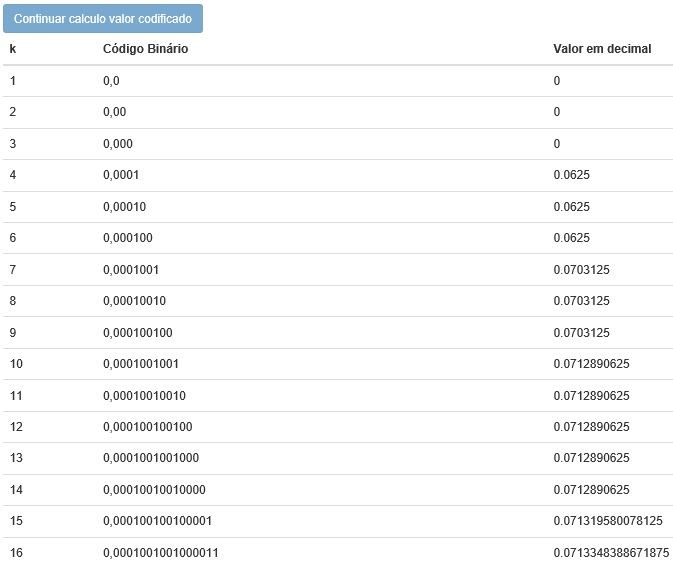
O código binário resultante neste exemplo será 0,0001001001000011 (16 bits) que corresponde ao decimal 0,00713348389.

Descodificação

A mensagem “UUSSAC?” que foi codificada anteriormente pelo algoritmo de codificação aritmética que originou um código binário com 16 bits e que o número decimal correspondente é 00713348389, dadas as probabilidades dos símbolos, inicia-se o processo de descodificação atribuindo um índice a cada símbolo do alfabeto, ao qual se associa uma probabilidade cumulativa probcum. Foram obtidos os seguintes valores:

Fig. 6 Tabela do descodificador para este exemplo

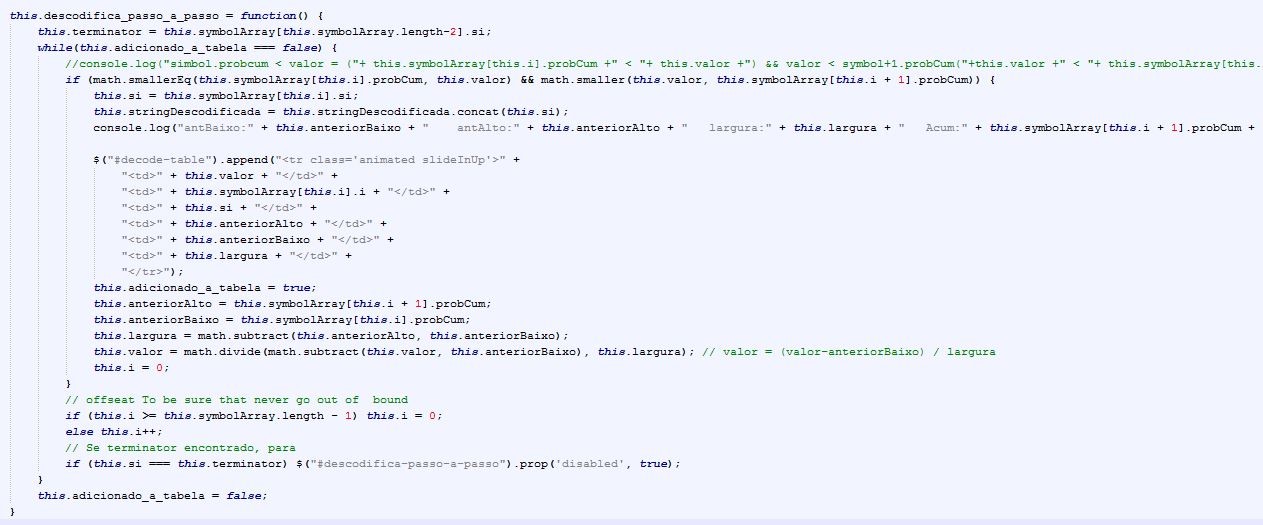
Aplicando o algoritmo do descodificador aritmético apresentado na Figura 3  obtemos os sub intervalos que correspondem a cada símbolo através da informação  presente na tabela da Figura 4 até chegar ao símbolo “?” que funciona como terminador do processo de descodificação.

Implementação do algoritmo de codificação aritmética

A nossa aplicação tem como base JavaScript, permite-nos integrar com diversas plataformas, principalmente WEB. Esta encontra-se composta por duas secções distintas, Codificação e Descodificação.

Uma das dificuldades encontrada na implementação desta aplicação, foi a elevada precisão matemática que o algoritmo de compressão aritmética exige.

Com Javascript puro não seria possível implementar este algoritmo. Para tal recorremos a uma libraria matemática chamada MathJS (math.js) – a libraria mais completa relacionada com problemas matemáticos em javascript. Esta suporta o tipo de dados BigNumber (decimal.js), que é um tipo de dados decimal com precisão arbitraria para javascript.

Desta forma é possível definir o numero de bits de precisão necessária para o problema (no nosso caso, foram utilizados 64 bits de precisão, podendo este valor ser alterado posteriormente). Quantos mais bits de precisão forem utilizados, mais lentos serão os cálculos, mas o valor obtido será mais preciso.

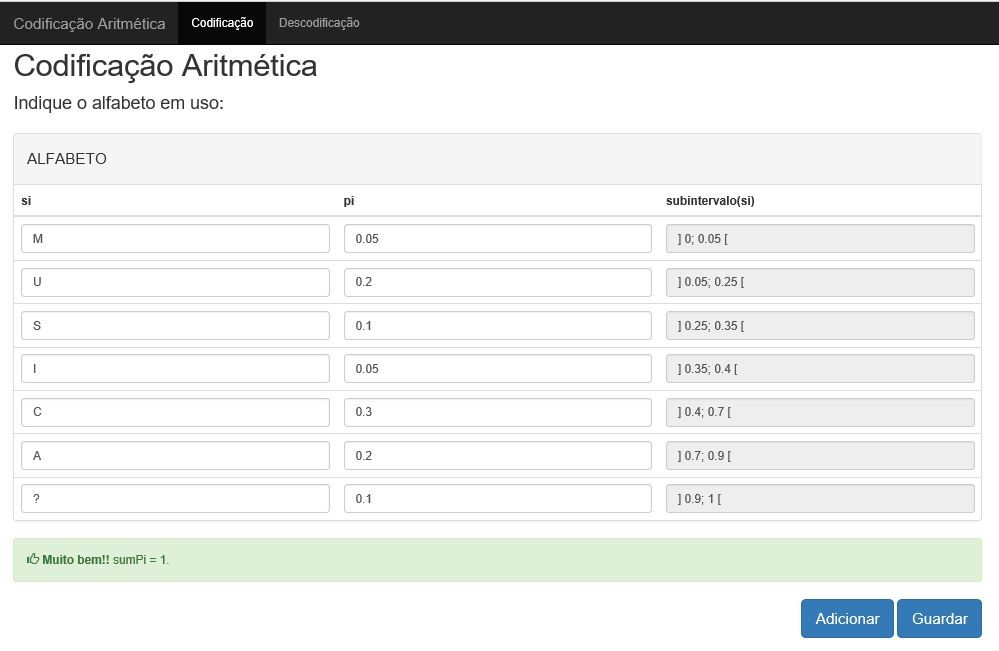
Na plataforma web, como mostraremos de seguida, podemos verificar que se encontra uma tabela que se vai adaptando às necessidades do Alfabeto pretendido, ou seja, caso seja necessário 3 símbolos esta tabela permite criar 3 linhas, caso sejam necessárias mais linhas bastara simplesmente selecionar através de um botão a quantidade destes.

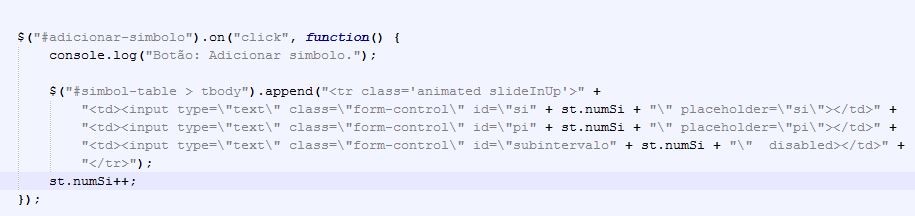
Esta implementação for feita recorrendo a jQuery, uma libraria popular para scripting no lado do cliente. Ela permitiu-nos manipular facilmente o DOM da página HTML.

Exemplo de utilização JQuery (código botão adicionar linha á tabela):

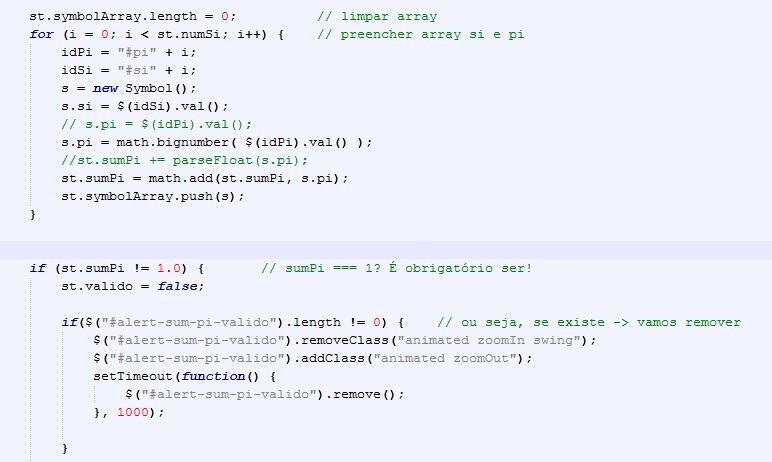
Portanto, o utilizador deverá adicionar as linhas necessárias e posteriormente preencher a tabela com os respetivos símbolos e probabilidades, caso por engano ou mesmo erro as probabilidades não fiquem de forma correta, ou seja, igual a 1, irá ser alertado dessa anomalia, podendo assim ajustar esse ou esses valor que se encontrem errados, por fim deveremos guardar a nossa tabela.

A validação de probabilidades é efetuada através do seguinte código:

Depois teremos o local para colocar o Alfabeto que pretendemos comprimir e deveremos guardar.

Para se iniciar a codificação deveremos sempre de forma inicial, solicitar o início de codificação, e de forma iterativa ir selecionando as vezes necessárias para a finalização do cálculo.

Por fim para o cálculo do valor em binário mais curto e fecho deste processo de codificação será necessário ir de forma iterativa selecionar o botão de cálculo valor codificado até que não sejam apresentados mais valores.

Para tal, o algoritmo utilizado foi o seguinte:

K=1;
Código_binario =0;
While(valor_decimal(cod_binario<LOW))
{
Atribuir 1 ao K-ésimo bit fracionário do Cod. Binário
If (valor_decimal(cod_Binario)<HIGH)
{
Passar K-ésimo bit a 0;
}
}

Na descodificação o utilizador deverá preencher a tabela de símbolos com as probabilidades acumuladas.

A validação da probabilidade acumulada é verificada, sendo o utilizador notificado caso exista uma anomalia ou erro no seu somatório, esta validação é efetuada utilizando javaScript para o cálculo e Jquery para manipulação do HTML.

Depois de construída a tabela, o utilizador introduz o código Aritmético (Binário), a descomprimir, sendo posteriormente de descodificação calculada automaticamente através do seguinte algoritmo:

Codificação e Descodificação Aritmética em javascript

Comparação com outros métodos semelhantes

Comparando a codificação aritmética com a codificação de Huffman que é outro método de compressão sem perda com elevado rácio, podemos dizer que a codificação aritmética é bem mais complexo que o método de Huffman pois codifica uma sequência de dados de entrada num único código enquanto que Huffman trata cada símbolo individualmente e atribui-lhe um código binário respectivo.

A codificação aritmética quanto maior for o tamanho da sequência de dados a comprimir mais se aproxima do valor de Entropia enquanto que se o alfabeto for grande, a probabilidade máxima é baixa e portanto o código de Huffman  comporta-se melhor que a codificação aritmética.

Uma grande vantagem da codificação aritmética é a facilidade de se implementar sistemas com múltiplos codificadores aritméticos.

Conclusão

Podemos verificar que a codificação aritmética apesar de ser um metódo complexo produz resultados satisfatórios no que diz respeito ao rácio de compressão para grandes fluxos de entrada de dados.

Embora seja um método de compressão que apresenta uma boa performance não é utilizado em projectos open-source ou mesmo aplicações comerciais pois é um algoritmo patenteado, ou seja, a sua inclusão em projetos iria incutir custos extra no desenvolvimento e venda dos mesmo. Por esse facto muitas vezes em vez da codificação aritmética é usado o algoritmo de codificação de Huffman, pois não é patenteado embora na maioria dos casos apresente um performance inferior à codificação aritmética compensa pelo facto que não acresce custos ao projeto a desenvolver .

Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.

Texto da autoria de Gil Pinto (27437), Stephanie Pinto (27221), Richard Pereira (22475) e revisto por Nuno Magalhães Ribeiro.

Código java da autoria de Gil Pinto (27437), Stephanie Pinto (27221), Richard Pereira (22475).

Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.