Introdução

A codificação de Golomb é um sistema de compressão de dados inventado por Salomon W. Golomb em 1966 que pode ser utilizado na compressão de dados em substituição ao código de Huffmann, apresentando resultados ótimos para determinadas distribuições de probabilidade dos símbolos codificados.

O sistema é baseado em codificação de entropia e tem como objetivo codificar números inteiros não negativos em que se verifica que a probabilidade de ocorrência é menor quanto maior for o número.

A codificação de Rice foi inventada por Robert F. Rice e consiste numa adaptação da codificação de Golomb.

Rice utilizou a codificação de Golomb e modificou-a de forma a que um parâmetro (mais tarde denominaremos esse parâmetro por ‘m’) passa-se a ser uma potência de 2, em vez de ser um número inteiro positivo.

Este método irá simplificar a codificação e possivelmente acelerar a implementação, no entanto, dependendo dos casos, o rácio de compressão poderá ser menor.

Áreas de aplicação

Existem inúmeros codecs de imagem e de áudio sem-perdas que utilizam a codificação de Golomb-Rice.

Normalmente esta codificação é usada na representação de valores diferenciais entre as previsões e o real.

JPEG-LS (imagem), FELICS (imagem), Apple Lossless (áudio) são exemplos de codecs que utilizam a codificação de Golomb-Rice.

Codificação de Golomb-Rice

Codificação

A codificação de Golomb-Rice tem como vantagem ser simples e de entendimento fácil.

Esta codificação aplica-se a todos os números ‘n’ inteiros não negativos e que vão depender de um parâmetro ‘m’ que deve ser previamente calculado.

• Primeiro começa-se por obter a sequência de bits que queremos codificar usando a codificação de Golomb-Rice.

• De seguida vamos calcular o parâmetro ‘m’ usando a probabilidade ‘p’ de encontrar um bit ‘0’ na sequência anteriormente obtida.

• Nota: Para Golomb-Rice, ‘m’ vai ser arredondado á potência de 2 mais próxima do valor original.

• Obter ‘n’ e calcular o coeficiente ‘q’ usando a fórmula

• Transformar ‘q’ em unário (ex. 4=11110, 1=10, 2=110)

• Calcular o resto ‘r’ e o parâmetro ‘c’ usando as seguintes fórmulas

• Na codificação de Golomb original existe um ‘passo’ extra. Esse passo consiste numa verificação:

• Se ‘r < 2^c –m’, ‘r’ é codificado como um inteiro sem sinal em ‘c–1′ bits.
• Se ‘r ≥ 2^c –m’, ‘r’ é representado como o inteiro sem sinal ‘r+2^c –m’ em ‘c’ bits.

• Como em Golomb-Rice o parametro ‘m’ é uma potência de 2, não é necessário fazer esta verificação visto que em todos os casos ‘r’ vai ser maior ou igual a ‘(2^c –m)’.

• Ou seja, em Golomb-Rice ‘r’ é sempre representado como ‘r+2^c –m‘ usando ‘c‘ bits.

• Finalmente o código será uma concatenação do coeficiente em unário ‘q‘ com ‘r‘      ->       (r+2^c –m).

Algoritmo de codificação em pseudo-código

c <- log2(m)

read n

q <- n/m

r <- n – q * m

for i <- 1 to q

write 1

write 0

b <- binary(r)

write b

Exemplo de Codificação

Exemplo 1

• „Sequência Bits       ->       000001001100010100000111010001

• „Subsequência de 0’s       ->       5 2 0 3 1 5 0 0 1 3 0 (ultimo ‘0’ usado para indicar que a sequência acaba com bit ‘1’)

• „p(0) = 20/30 = 0,7

• m„ = ⌈ -log(1+p)/log(p) ⌉ = ⌈ –log(1,7)/log(0,7) ⌉ = 2

• q = ⌊ n/m ⌋ = ⌊ 5/2 ⌋ = 2       ->       110 (unário)

• r„ = n – qm = 5 – 2 * 2 = 1

• c = ⌈ log₂m ⌉ = ⌈ log₂2 ⌉ = 1

• „Como ‘m’ é uma potência de 2 então r ≥ 2^c –m

• „r + 2^c –m = 1 + 0 = 1       ->       (1)1

• „n=5 vai ser codificado com a concatenação de ‘q’ e ‘r’       ->       110 1
  

• E assim sucessivamente para o resto das subsequências de 0’s

• No final vamos ter a seguinte sequencia codificada       ->       1101|100|00|101|01|1101|00|00|01|101|00

Exemplo 2

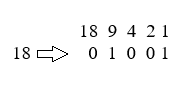
Imaginemos que num determinado ficheiro de áudio ou de imagem o primeiro byte corresponde ao valor 18.

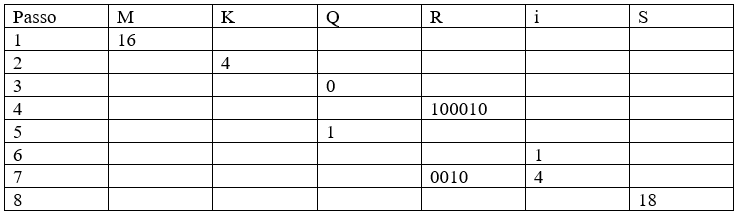
Resultado da aplicação de cada um dos passos do algoritmo de codificação (compressão) recorrendo ao exemplo introduzido acima.

Para m= 16, começamos por determinar o valor de K:

K = log2(16) = 4

Imaginemos agora que temos um ficheiro onde o primeiro byte tem o valor de 18. Vamos atribuir ao S esse mesmo valor:

Read(s) ,  S = 18

Agora, vamos converter o 18 em binário:

Logo 18 em decimal = 10010 em binário

Como 1 byte tem 8 bits acrescenta-se mais 3 zeros: 00010010

Em seguida, vamos determinar o valor do Quociente (Q):

Q = S >> K (Logical Shift Right)

Q = 00010010 >> 4  (Shift Right de 4 posições)

Q = 0001, a representação de Q em unário é 10. Ignoram-se os zeros à esquerda e acrescenta-se um zero no fim.

Determinar agora o valor de R:

R = S AND (M-1) (AND é uma operação lógica)

M-1 = 16-1 = 15

15(decimal) = 1111 (binário)

Calcular o R:

Nota: As regras dizem que o R deve ser representado com K bits. Neste caso K=4, logo:

R = 0010

Por último, o algoritmo vai percorrer um ciclo for de 1 até Q. Neste caso, Q=1 logo o numero 1 só irá ser impresso uma vez. De acordo com a codificação, à saída do ciclo irá ser impresso um zero.

Os números obtidos no passo anterior devem ser concatenados a R, ou seja:

Valor de Saída = ‘10’+’0010’ = 100010

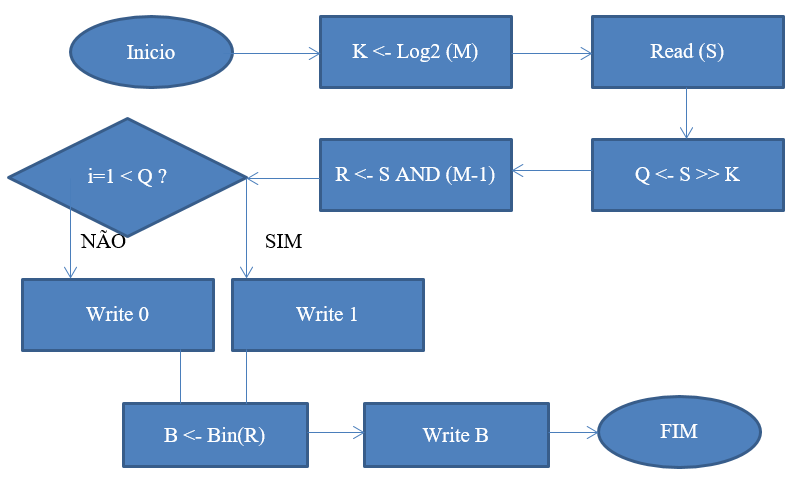
Fluxograma (Codificação)

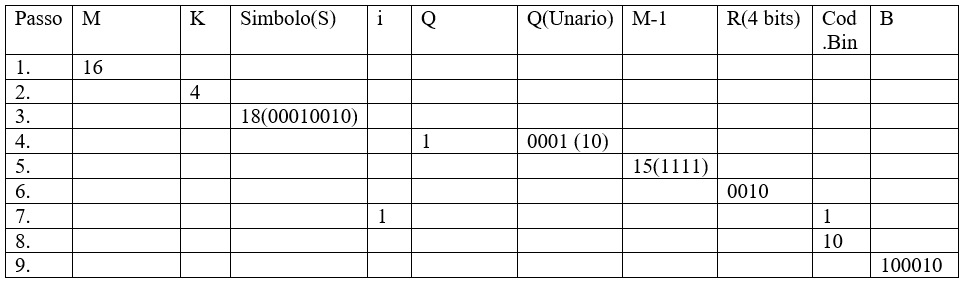
Traçagem (Codificação)

Descodificação

A codificação de Golomb-Rice foi feita de forma a facilitar a sua descodificação.

No algoritmo de descodificação, os valores de ‘q’ e ‘r’ são usados para reconstruir o valor original ‘n’ utilizando a formula que já tinhamos visto:

Em ordem a ‘n’ fica       ->       n = r + qm

• Começamos a descodificação por calcular o valor de ‘c‘ usando a fórmula:

• Posteriormente calculamos o número de bits 1’s até encontrar um bit ‘0’ (que será o valor de ‘q’ em unário).

• Na codificação de Golomb original temos de fazer mais uns ‘passos extra’ para calcular o valor exato de ‘r’:

• Os seguintes c-1 bits vão ser r1
  • Se r1 < 2^c –m, então o comprimento total do código é ‘q + 1 + (c − 1)’ (os ‘q’ 1’s, o ‘0’ seguinte e os ‘c − 1′ bits seguintes) e seu valor é ‘ m × q + r1 ‘.
  • Se r1 ≥ 2^c –m, então o comprimento total do código é q + 1 + c e seu valor é ‘ m × q + r – (2^c –m)’, onde ‘r‘ é o inteiro de ‘c‘ bits formado por r1 e pelo bit seguinte ao r1.

• Isto deixa de ser necessário na codificação de Golomb-Rice visto que ‘r’ vai ser sempre os ‘c’ bits a frente do primeiro ‘0’ que encontramos.

• O comprimento total do código será dado por       ->       q + 1 + c

• E ‘n‘ será obtido pela formula       ->       n = m × q + r – (2^c –m).

Algoritmo de descodificação em pseudo-código

c <- log2(m)

q <- 0

r <- “”

while Readbit =1

q <- q + 1

for i <- 1 to c

r <- concat(r, Readbit)

n <- q * m + r – (2^c – m)

write n

Exemplo de descodificação

Exemplo 1

Descodificar 1101 usando m = 2

• c = ⌈ log₂m ⌉ = ⌈ log₂2 ⌉ = 1

• Calcular 1’s antes de aparecer o primeiro ‘0’       ->       q = 2

• Chamar de ‘r’ os ‘c’ bits seguintes (visto que ‘m’ é potência de 2)       ->       r = 1

• O comprimento do código é dado por       ->       q + 1 + c = 4

• n = m * q + r – (2^c –m= 2 * 2 + 1 – 0 = 5

Exemplo 2

Resultado da aplicação de cada um dos passos do algoritmo de descodificação (descompressão) recorrendo ao exemplo introduzido acima.

Para a descodificação, vamos utilizar em R o valor final que foi obtido na codificação.

R = 100010

Para m= 16, vamos calcular novamente o K:

K = log2(16) = 4

No próximo passo do algoritmo, temos um ciclo do while que vai contar 1’s em R enquanto não encontrar um zero. Se não encontrar zeros, incrementa +1 na variável Q, caso contrário termina o ciclo. Neste caso, Q=1.

Em seguida, um ciclo for de i=1 até K=4 onde vai ser concatenado a R o valor do readbit. Neste caso, R=0010 que corresponde ao código binário onde foi interrompido o ciclo while anterior.

O ultimo passo consiste em obter o S(Simbolo), que foi o valor dado no exemplo da codificação.

 S = Q * M + R

S = 1 * 16 +2 = 18

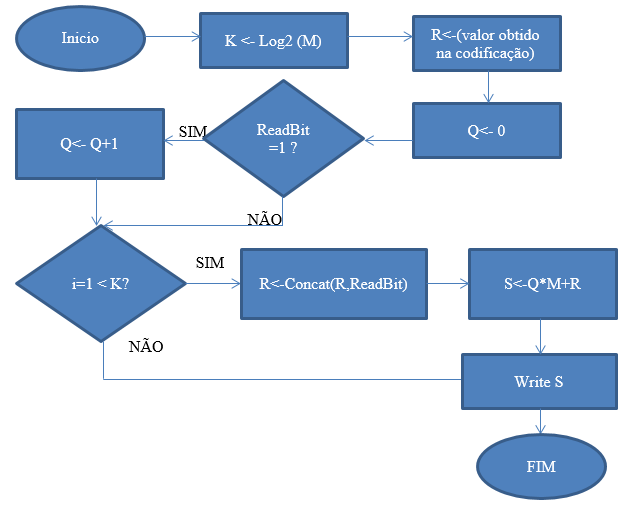
Fluxograma (Descodificação)

Traçagem (Descodificação)

Comparação com outros métodos semelhantes

No gráfico 1 é comparado o rácio de compressão da codificação Golomb-Rice com o método deflate (que utiliza o algoritmo de compressão LZ77 e o algoritmo de Huffman).

Da análise do gráfico 1 podemos concluir que a codificação de Golomb-Rice obtem um rácio de compressão maior em valores próximos de ‘0’.

Gráfico 1 – Compressão sem perda de imagens utilizando a codificação de Golomb-Rice

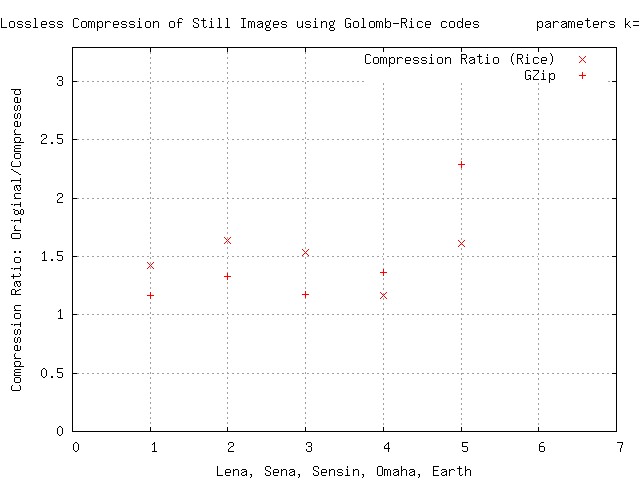
fonte: http://en.wikipedia.com/wiki/Golomb_coding

Para valores maiores, o método deflate apresenta valores de compressão melhores pelo que, nestes casos, é desaconselhado o uso da codificação de Golomb-Rice.

Conclusão

Para valores muito pequenos de p, tais como 0.1, dão origem a uma sequência com mais 1’s do que 0’s. Neste caso, a codificação de Golomb-Rice pode ser usada para comprimir subsequências de 1’s.

Para valores de ‘p’ em torno de 0.5, a codificação de Golomb-Rice não é uma boa escolha e outros métodos devem ser considerados (por ex. Algoritmo de Huffman).

Verificamos que a codificação de Golomb-Rice apresenta uma codificação simples, eficaz e uma descodificação rápida.

A codificação de Rice é mais aplicada do que a codificação de Golomb original visto que ‘m’ sendo uma potência de 2, acelera e simplifica muito o processo de codificação e descodificação.

Bibliografia

Website – http://en.wikipedia.org/wiki/Golomb_coding

Website – http://pt.wikipedia.org/wiki/Códigos_de_Golomb

Azevedo, R., “Trabalho Multimedia” 2008

Mendonça, N., Moreira, P., “Trabalho Multimedia” 2013

Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.

Texto da autoria de Miguel Ferreira (nº 27256) e Diogo Fernandes e revisto por Nuno Magalhães Ribeiro.

 

Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.