O Algoritmo

O PPM, ou Prediction by partial matching, é um método originalmente desenvolvido por J.Cleary e I.Witten. Este método baseia-se num codificador que mantém um modelo estatístico do texto. Nesse modelo é tido em consideração o contexto do símbolo para que se possa atribuir-lhe uma probabilidade e esta ser enviada para um codificador aritmético adaptativo.
Na prática o contexto de um símbolo corresponde aos ‘N’ símbolos precedentes. Este método pode ser encarado como um método de pré-processamento, visto ser uma preparação dos dados de input que posteriormente serão utilizados pelo codificador aritmético adaptativo.

Os princípios do algoritmo PPM

O algoritmo PPM, na sua forma mais simplista, propõe para um dado símbolo ‘S’ de entrada lhe seja atribuída uma probabilidade ‘P’, para que ‘S’ seja enviado para um codificador aritmético adaptativo e codificado com probabilidade ‘P’. O modelo estatístico contará o número de vezes que o símbolo ocorreu anteriormente e em que contexto, atribuindo-lhe a respectiva probabilidade. Desta forma é possível atribuir uma probabilidade ao símbolo que não dependa apenas da frequência absoluta mas também no contexto em que ocorreu.
A ideia chave do PPM é utilizar o seu conhecimento, onde para isso inicia-se com um contexto de ordem-N. O codificador PPM troca para um contexto menor, ordem-N-1, quando a probabilidade é ‘0’, isto é, o símbolo nunca foi visto na estrutura de dados anteriormente, no contexto em que se encontra.
A um nível mais detalhado o codificador lê o símbolo ‘S’ seguinte, verifica a sua ordem-N de contexto, e baseado nos dados de input, que foram vistos no passado, determina a probabilidade ‘P’ que ‘S’ irá aparecer seguido daquele contexto particular. O codificador nesta fase invoca um codificador aritmético adaptativo de modo a codificar o símbolo ‘S’ com probabilidade ‘P’. A probabilidade de um carácter ‘X’ no contexto de ‘S’ pode ser descrita da seguinte forma: C (X|S) /C (S), onde C (X|S) é o número de vezes que o carácter ‘X’ seguiu-se da string ‘S’ e C (S) é o número de vezes que ‘S’ aparece [1].
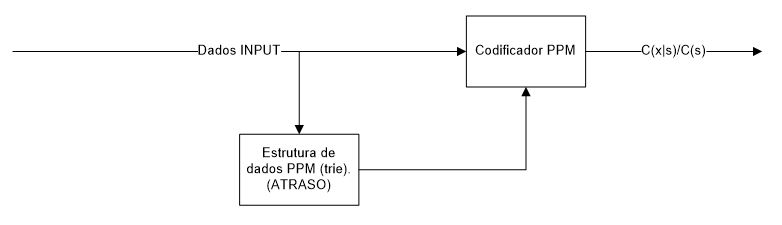
Como já foi referido inicialmente, o PPM é um método de pré-processamento, que pode ser considerado com o seguinte diagrama de blocos da Figura 1.

Figura 1 – Diagrama de blocos do algoritmo PPM

Como se pode verificar o bloco PPM recebe os dados de input, e à medida que vai calculando as respectivas probabilidades, envia-as para o codificador aritmético adaptativo, de modo a este produzir os respectivos códigos.

Focalizando a atenção no bloco PPM, podemos detalha-lo conforme o diagrama de blocos da Figura 2.

Figura 2 – Diagrama de blocos de detalhe do PPM

Neste diagrama podemos verificar o bloco de atraso, que é na prática utilizado para criar a estrutura de dados (uma árvore denominada de trie) necessária para que seja possível gerar as respectivas probabilidades.

À medida que os dados de input vão chegando, o codificador PPM com a ajuda da árvore que está se ser criada on-the-fly, pesquisa nessa estrutura de dados nos respectivos contextos as ocorrências, enviado assim a respectiva probabilidade a ser processada para um dado carácter ‘X’, num determinado contexto.

O Algoritmo PPM

O algoritmo PPM é talvez dos algoritmos que consegue obter dos melhores rácios de compressão, contudo não é dos mais rápidos. O algoritmo pode ser delineado em quatro passos [2].

1º Encontrar ocorrências múltiplas de strings de tamanho N (onde N é o valor de uma constante definida).

2º Ao que sobrar, tentar encontrar outras ocorrências de strings de ordem N-1.

3º Repetir até que todas as combinações possíveis tenham sido encontradas e lhe tenham sido atribuídas a respectiva probabilidade a cada string de acordo com a sua ocorrência.

4º Enviar as probabilidades obtidas para o codificador aritmético adaptativo.

A Estrutura de dados do PPM

Para manter uma estrutura de dados que preserve todos os contextos, de ordem-0 até N, dos símbolos lidos, a estrutura que se segue é um tipo de árvore especial, denominada de trie. Este tipo de árvore cresce principalmente em largura, dependendo da ordem de contexto, p.ex,: se tivermos ordem-2, a árvore não terá mais que N+1 de altura, independentemente da quantidade de dados lidos, isto é, para este exemplo não mais que 3 níveis de altura (a raiz não conta como nível). O primeiro nível da trie, logo abaixo da raiz, é o que contém apenas um nodo para cada símbolo lido até então, estes são os contextos de ordem-1. No nível 2 contém, então, todos os contextos de ordem-2 etc. Na trie cada nodo contém o número de ocorrências, ou seja, no caso do nível 1, esse número, significa que o símbolo ‘S’ ocorreu ‘X’ vezes no total, no caso do nível 2, significa que o símbolo ‘S’ ocorreu ‘X’ vezes seguido do contexto que se encontra.

Figura 3 – Exemplo de uma TRIE para a string “zxzyzxxyzx”. [3]

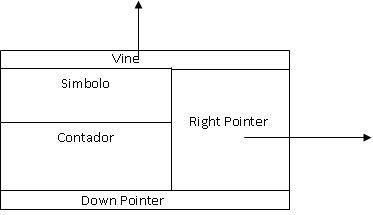
A árvore, trie, é constituída por folhas, ou nodos, cada um desses nodos pode ser caracterizado da seguinte forma [3]:

• O código ASCII ou qualquer outro, do símbolo.
• Um contador.
• Um apontador para baixo (down pointer) que aponte para o filho esquerdo desse nodo (folha).
• Um apontador para a direita (right pointer) que aponte para nodo sequinte à direita (next sibling). A raiz não tem nodo à direita.
• Um apontador vine, apontador esse que aponta para trás.

Figura 4 – Estrutura de um nodo (folha) de uma TRIE.

O passo seguinte, que será visto, é como o algoritmo decide que nodos actualizar e quais adicionar. Para simplificar o algoritmo o apontador vine aponta para trás, ou seja, para uma ordem de contexto inferior, ordem N-1. Durante a construção desta árvore será preservado um outro apontador, que se chama apontador base. Este apontador é o que irá apontar sempre para o último nodo adicionado ou actualizado. O algoritmo para adicionar/actualizar os nodos então é o seguinte [3]:

• Posicionar-se no nodo ao qual o base aponta. Seguir o ponteiro vine desse nodo até a um dado nodo Y (Y poderá ser a raiz). Adicionar S (o novo símbolo) como novo filho do nodo Y e colocar a base a apontar para este nodo inserido. Contudo, se o nodo Y já tiver um filho igual a S incrementa-se o contador do mesmo, em uma unidade, e actualiza-se, na mesma, o apontador base para ele. Chame-mos este novo nodo inserido, ou apenas actualizado, nodo A.
• Repetir o passo anterior, mas agora sem actualizar o apontador base. Seguir o apontador vine do nodo Y para um dado nodo Z, adicionar S como novo filho de Z. Se Z tem um filho com S incrementar apenas o contador em uma unidade desse filho. Chame-mos este nodo inserido ou actualizado B. Se não existir uma ligação do apontador vine de A para o nodo B criar essa ligação, apontando o vine de A para o nodo B. (Se estes nodos são antigos, certamente já existe essa ligação).
• Repetir até que se tenha adicionado (ou incrementado) um nodo no nível 1 da árvore, ou seja ordem-1 de contexto.

Exemplo de inserção na estrutura de dados

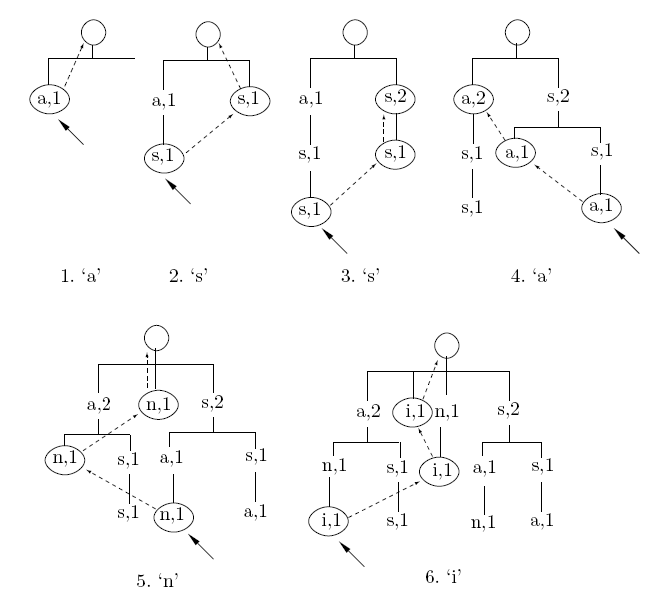
De forma a perceber melhor este algoritmo de inserção, na trie, será demonstrado de seguida um exemplo para a string “assani” cuja ordem de contexto é 2. Essa demonstração será no sexto passo quando o carácter “i” é inserido. De notar que o algoritmo de actualização/inserção nos primeiros passos, quando a árvore não atinge a altura máxima (N+1), não se aplica, ficando a implementação desses primeiros passos à descrição de quem implementa esta estrutura de dados.

Figura 5 – Árvore (trie) da string “assani”. [3]

No sexto passo quando o carácter de entrada, nomeadamente o “i”, é recebido, segue-se o apontador vine (seta tracejado) do base (assinalado pela seta no 5º passo), de onde se verifica que o nodo (n,1) não tem nenhum filho, portanto o apontador down do nodo ‘n,1’ é nulo. Se então não tem nenhum filho adiciona-se o novo nodo como filho desse. O novo nodo será o ‘i,1’. Após adicionar esse mesmo nodo este será a nova base (conforme indicado no 6º passo da fig.5).

Continuando a subir, segue-se o vine do nodo, ao qual se inseriu o filho. O vine desse é então o ‘n,1’, como se pode verificar na fig.5 seguindo as setas tracejadas. O mesmo processo é executado mas agora sem actualizar a base. Verificamos então que este não tem filho e adiciona-se um novo nodo. No fim deste passo aponta-se então o vine da base para este novo nodo inserido (nova base já definida logo na primeira etapa (i,1)).

Subindo mais um nível (nível 1, seguindo as setas a tracejado) encontramo-nos na raiz, raiz essa que já tem vários filhos, de onde se pesquisa de modo a analisar se já existe algum filho com o carácter “i”. Neste caso não existe, logo insere-se o novo nodo, e coloca-se o apontador vine do último nodo inserido (o do passo anterior) a apontar para este. O processo termina neste passo visto que já se adicionou um nodo no nível 1.

Eficiência do PPM: comparação entre as implementações PPMD e PPMZ

O PPM é um algoritmo que consegue atingir bons rácios de compressão graças ao seu modelo estatístico, bem como, ao codificador aritmético, de que faz uso, contudo não é dos codificadores mais rápidos a comprimir, sendo esse talvez o aspecto menos positivo deste método de compressão.

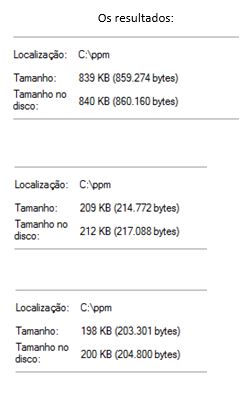
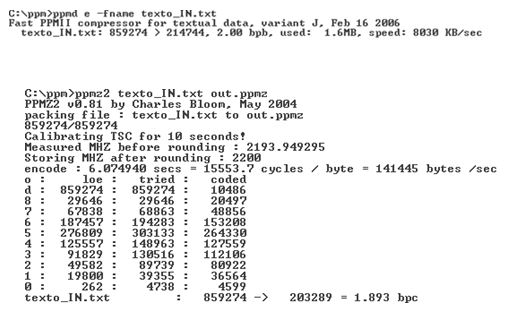
De forma a demonstrar que rácios de compressão é possível obter com este algoritmo, segue-se alguns resultados obtidos, testados em implementações de duas variantes do PPM, nomeadamente o PPMD [4] e o PPMZ [5]. Estas variantes seguem a base do PPM, onde inovam apenas em aspectos mais centrados no desempenho (velocidade de codificação), estrutura de dados da trie, bem como o princípio de exclusão que não foi abordado neste relatório, portanto a essência mantêm-se.

Como se pode verificar o PPMD obteve um rácio de 4.00086 com um comprimento médio de 2 bits por caracter, já o PPMZ conseguiu atingir um rácio de 4.22661 com um comprimento médio de bits por caracter de 1.893. Em contrapartida o PPMZ foi o que demorou mais tempo a codificar, aproximadamente 6.07 seg (141445bytes/seg ~ 138.13KB/seg), já o PPMD foi praticamente instantâneo (8030KB/seg), uma vez que esta variante opta por uma implementação de fast PPM.

Pode-se concluir que para obtenção de melhores taxas de compressão mais complexo e lento se torna o algoritmo.

Conclusão

O algoritmo apresentado é sem dúvida um excelente método de compressão, sem perdas, que consegue atingir óptimos rácios de compressão e com um número médio de bits por carácter muito próximos da entropia, uma vez que para além de tirar partido de um excelente modelo estatístico, tendo em conta sempre o contexto em que o caracter aparece no texto, faz uso do codificador aritmético adaptativo. Claro está, que como foi demonstrado com as variantes do PPM, quanto mais complexo se torna o algoritmo, de modo a obter melhores rácios de compressão, mais lenta a codificação se torna.

Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.

Texto da autoria de Ricardo Caló Santos e Nelson Ferreira e revisto por Nuno Magalhães Ribeiro.

Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.