Introdução
O método de compressão de Burrows-Wheeler, é um algoritmo que é usado nas técnicas de compressão como por exemplo o Bzip. Foi inventado por Michael Burrows e David Wheeler em 1994. Foi baseado numa pesquisa (não publicada) de Wheeler em 1983. É um dos melhores algoritmos de compressão global para o texto.
No inicio, submetemos os dados na função de transformação, a “Burrows-Wheeler Transform”, ou simplesmente BWT, que vai reordenar os bytes originais, e vai torna-los bastante propícios para a compressão.
Depois, aplicamos o “Move To Front”, ou simplesmente MTF. O MTF melhora a entropia entre os métodos de compressão. Quando é aplicado eficazmente, facilmente se vê que os resultados justificam a aplicação deste passo extra nos algoritmos de compressão. Aplicar o MTF logo após o BWT faz com que os dados de saída tenham muitos zeros e uma grande tendência para ter números positivos pequenos.
Codificação
Ao contrário dos algoritmos da família “LZ”, o BWT funciona com blocos de dados, e não em “streams” que lêem poucos dados de cada vez. Quanto maior é o tamanho dos blocos, maior vai ser a taxa de compressão atingida.
Parâmetros de entrada: um vector A de tamanho N com os dados a serem transformados
Parâmetros de retorno: um vector B (permuta dos elementos de A) e um índice k
Inicialmente, são geradas todas as N rotações à direita possíveis para o vector A, formando uma matriz N x N. A seguir, ordenamos estas N linhas e copiamos o último caracter de cada uma para o vector B. Atribuímos a k o número da linha da matriz ordenada que corresponde à A.
Descodificação
O problema permanece, no entanto, de como reconstruir a sequência original da sequência codificada. A maneira de fazer isso é a contribuição genial feita por Burrows e Wheeler. A ordem dos caracteres mais significantes no contexto ordenado desempenha um papel importante na descodificação.
Uma vez que os contextos são classificados em ordem lexicográfica inversa, conjuntos de contextos cujos caracteres mais significantes são iguais, serão ordenados pelo restante contexto, ou seja, a sequência de todos
anterior caracteres. Se abandonarmos o caracter menos significativo desses contextos, então eles são exactamente o mesmo que o contexto restante
acima, e, portanto, serão classificados na ordem do mesmo. A única vez que deixar cair o caracter menos significante pode fazer a diferença é quando todos os outros caracteres são iguais. Isso só pode acontecer quando todos os caracteres na entrada são iguais.
Descrição mais detalhada da Transformada de Burrows-Wheeler
Introdução
O algoritmo da Transformada de Burrows-Wheeler foi inventado por Michael Burrows e David Wheeler em 1994. A implementação do método é simples e rápida.
O algoritmo de codificação manipula os símbolos de S, a sequência original de entrada, através de várias permutações entre si. O processo de descodificação transforma a sequência de volta para a original. Durante o processo de codificação, toda os símbolos da sequência de entrada são permutados, e a nova sequência contém, com esperança, algumas características benéficas para a compressão.
A maioria dos métodos de compressão operam em modo de streaming, onde o codec insere um byte, ou vários bytes, processa-os, e continua até um EoF (end-of-file). A Transformada de Burrows-Wheeler, no entanto, opera por “blocos”, onde o fluxo de entrada é lido bloco a bloco, e cada bloco é codificado separadamente como uma única string. É portanto referido como block sorting.
A Transformada tem uso geral, isto é, funciona bem em imagens, som e texto, e pode obter rácios de compressão bastante elevados (1 bit por byte ou melhor).
Ainda importante, a transformada é reversível, sem ser necessário armazenar dados adicionais.
Áreas de aplicação
O algoritmo da Transformada de Burrows Wheeler é a base de alguns softwares de compressão de dados, tais como o bzip, e até de software da área das ciências biomédicas, para codificar e compactar informação de sequências de ADN.
O algoritmo da Transformada de Burrows-Wheeler
Codificação
O objectivo deste processo é reordenar os símbolos de uma sequência de entrada S, para derivar L, uma nova sequência que irá permitir uma melhor compressão.
O comprimento do array original S, e do array resultante L é o mesmo porque L apenas é uma permutação de S. Noutras palavras, apenas queremos mudar a ordem dos símbolos do array original S para obtermos um novo array L que, se espera, seja comprimido mais eficientemente.
É claro que o novo array L não pode ser um qualquer array após algumas permutações aleatórias. Podem haver outras formas de reordenar um array mas a que é usada pela Transformada de Burrows-Wheeler funciona bem na práctica.
Derivar L
Para obtermos o array L, é necessário seguir os seguintes passos:
1) Primeiro, deslocamos a string S um símbolo para a esquerda num movimento circular, isto é, o símbolo mais à esquerda é deslocado para fora do array e é depois adicionado na direita, ficando assim como o elemento mais à direita no array. Por exemplo,
‘A C C E L E R A T E’ irá ficar ‘C C E L E R A T E A’ após uma única deslocação. Como podemos ver na figura abaixo.
Repetindo o passo acima n-1 vezes, podemos gerar uma matriz n x n onde n é o número de símbolos existentes no array, e cada linha e coluna é uma permutação de S.
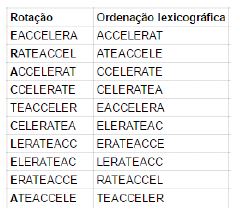
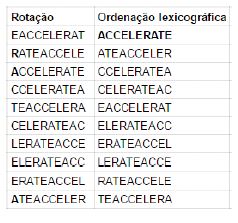
2) Agora, ordenamos as colunas da matriz por ordem lexicográfica, portanto, a matriz resultante fica:
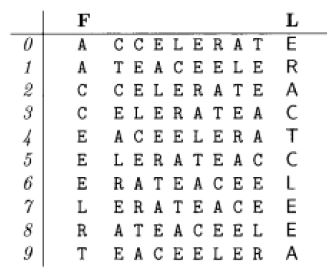
3) Agora, chamamos à ultima coluna L, que é o que precisamos na Transformada de Burrows-Wheeler para codificar, onde s1 indica o primeiro símbolo do array original S.
Observação: Se chamarmos à primeira coluna F, então F pode ser derivada de L apenas ordenando L lexicograficamente.
Descodificação
O objectivo do processo inverso da transformada é recuperar a string original S a partir de L.
Portanto é necessário seguir os seguintes passos:
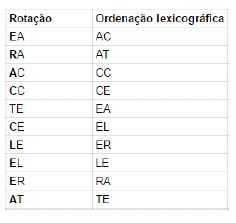
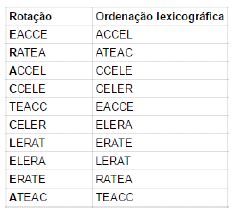
1) Escrevemos a string obtida, L, numa coluna, e na coluna ao lado a string F.
2) Em seguida adicionamos o array L à esquerda da string obtida após a ordenação lexicográfica. Por fim, voltamos a ordenar. Este processo repete-se n vezes (sendo n o número de símbolos do array S) até obtermos a string original S.
1ª iteração:
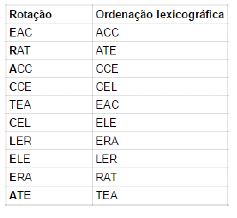
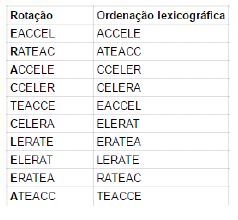
2ª iteração:
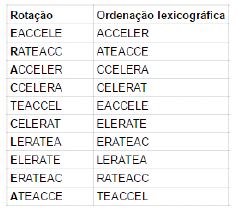
3ª iteração:
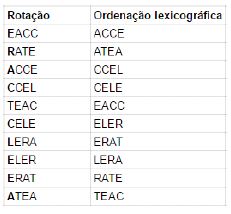
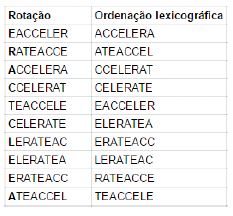
4ª iteração:
5ª iteração:
6ª iteração:
7ª iteração:
8ª iteração:
9ª iteração:
10ª iteração:
Implementação do algoritmo da Transformada de Burrows-Wheeler
Para a implementação do algoritmo da BWT foi usada a plataforma Java.
O algoritmo da codificação pode ser analisado a partir do seguinte pseudocódigo:
Função_bwt (String S) { //S = string de entrada
Criar uma tabela onde todas as linhas são permutações úncias da string S;
Ordenar as linhas da tabela alfabeticamente;
Retornar L; //a última coluna da tabela;
Guardar a posição da string original S na tabela;
}
Função_bwt_reverse (String L) {
Criar uma tabela vazia;
Repetir n vezes { //n é o número de caracteres na string
//a primeira inserção cria a primeira coluna
Inserir L como uma coluna da tabela à esquerda da primeira coluna da tabela;
Ordenar as linhas da tabela alfabeticamente;
}
Retornar a linha cuja posição corresponde à posição da string original na tabela criada em função_bwt;
}
Transformada de Burrows-Wheeler em java
Comparação com outros métodos semelhantes
Existem outros métodos semelhantes ou que podem funcionar em conjunto com a transformada de Burrows-Wheeler, tal como o RLE (Run-Length Encoding).
Como apenas estamos a estudar a parte da codificação e descodificação, não havendo nenhuma compressão, o número de bits de entrada vai ser igual ao número de bits de saída, não fazendo sentido calcular o rácio de compressão, que seria igual a 1.
Conclusão
Concluímos que a transformada de Burrows-Wheeler permite obter bons rácios de compressão.
Sendo que se trata de um algoritmo de entropia, pois recorre a compressão sem perdas, nenhuma informação codificada ou descodificada é perdida.
Bibliografia
Salomon, D. – “Data Compression”, Springer, 4th. Edition, 2002. http://www.cs.princeton.edu/courses/archive/spr03/cs226/assignments/burrows.html
Data Compression with the Burrows-Wheeler Transform. [Em linha]. Disponível em http://marknelson.us/1996/09/01/bwt/ ehttp://sites.google.com/site/compgt/bwt
Algoritmo Burrows-Wheeler. [Em linha]. Disponível em http://www.ime.usp.br/~fli/bwt.html e http://sites.google.com/site/compgt/mtf
Wikipédia. [Em Linha]. Disponível em http://en.wikipedia.org/wiki/Burrows%E2%80%93Wheeler_transform
Trabalho desenvolvido no âmbito da disciplina de Multimédia II da Licenciatura em Engenharia Informática, lecionada pelo Prof. Doutor Nuno Magalhães Ribeiro da Faculdade de Ciência e Tecnologia da UFP.
Texto da autoria de André Martins (28017), Filipe Laranjeira (26388), José Cunha (28018) e Luís Silva (24288) e revisto por Nuno Magalhães Ribeiro.
Código javascript da autoria de André Martins (28017), Filipe Laranjeira (26388), José Cunha (28018) e Luís Silva (24288).
Site planeado, desenhado, desenvolvido e programado por Daniel Dias Lima Mendes, Diogo Emanuel Lamas e Silva, Nelson José Santos Almeida no âmbito do Projeto de final de Licenciatura realizado na Unidade Curricular de Laboratório de Projeto Integrado sob a orientação técnica do Prof. Doutor Nuno Magalhães Ribeiro.